Question

How do you sketch one cycle of $y = \sec \left( {2x} \right)?$

Answer 1

We need to know the trigonometric table value for $\cos \theta$and$\sec \theta$. Also, we need to know the relation between $\cos \theta$ and $\sec \theta$. Also, this question involves the operation of addition/ subtraction/ multiplication/ division. Also, we need to know how to assume the $x$ value, by using the assumed $x$ value we can set $y$ the value. We need to know how to sketch graphs by using the $x$ and $y$ values.

Complete step by step solution:
The given equation is shown below,
$y = \sec \left( {2x} \right) \to \left( 1 \right)$
We know that,
$\cos \theta = \dfrac{1}{{\sec \theta }}$
So, first, we would find the value for $\cos \theta$, next, we can easily find the values for $\sec \theta$.
We get,
$\cos 2x = \dfrac{1}{{\sec 2x}}$
$\sec 2x = \dfrac{1}{{\cos 2x}} \to \left( 2 \right)$
We assume,
$x = ....\dfrac{{ - \pi }}{2},0,\dfrac{\pi }{2},\pi ,\dfrac{{3\pi }}{2},2\pi ,.....$
Let substitute $x = \dfrac{{ - \pi }}{2}$ in the equation $\left( 2 \right)$, we get
$\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}$

$$\sec \left( {2 \times \dfrac{{ - \pi }}{2}} \right) = \dfrac{1}{{\cos \left( {2 \times \dfrac{{ - \pi }}{2}} \right)}} = \dfrac{1}{{\cos \left( { - \pi } \right)}} = \dfrac{1}{1} \\\ \sec \left( {2 \times \dfrac{{ - \pi }}{2}} \right) = 1 \\\$$

Let substitute $x = 0$in the equation $\left( 2 \right)$, we get
$\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}$

$$\sec \left( {2 \times 0} \right) = \dfrac{1}{{\cos \left( {2 \times 0} \right)}} = \dfrac{1}{{\cos 0}} = \dfrac{1}{1} \\\ \sec \left( {2 \times 0} \right) = 1 \\\$$

Let’s substitute$x = \dfrac{\pi }{2}$in the equation$\left( 2 \right)$, we get
$\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}$

$$\sec \left( {2 \times \dfrac{\pi }{2}} \right) = \dfrac{1}{{\cos \left( {2 \times \dfrac{\pi }{2}} \right)}} = \dfrac{1}{{\cos \left( \pi \right)}} = \dfrac{1}{{ - 1}} \\\ \sec \left( {2 \times \dfrac{\pi }{2}} \right) = - 1 \\\$$

Let’s substitute $x = \pi$in the equation$\left( 2 \right)$, we get
$\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}$

$$\sec \left( {2 \times \pi } \right) = \dfrac{1}{{\cos \left( {2 \times \pi } \right)}} = \dfrac{1}{{\cos 2\pi }} = \dfrac{1}{1} \\\ \sec \left( {2 \times \pi } \right) = 1 \\\$$

Let’s substitute $x = \dfrac{{3\pi }}{2}$ in the equation$\left( 2 \right)$, we get
$\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}$

$$\sec \left( {2 \times \dfrac{{3\pi }}{2}} \right) = \dfrac{1}{{\cos \left( {2 \times \dfrac{{3\pi }}{2}} \right)}} = \dfrac{1}{{\cos \left( {3\pi } \right)}} = \dfrac{1}{{ - 1}} \\\ \sec \left( {2 \times \dfrac{{3\pi }}{2}} \right) = - 1 \\\$$

Let’s substitute $x = 2\pi$ in the equation $\left( 2 \right)$, we get
$\left( 2 \right) \to \sec 2x = \dfrac{1}{{\cos 2x}}$

$$\sec \left( {2 \times 2\pi } \right) = \dfrac{1}{{\cos \left( {2 \times 2\pi } \right)}} = \dfrac{1}{{\cos 4\pi }} = \dfrac{1}{1} \\\ \sec \left( {2 \times 2\pi } \right) = 1 \\\$$

By using these values we can make the following tabular column,

$x$	$\dfrac{{- \pi}}{2}$	$0$	$\dfrac{\pi}{2}$	$\pi$	$\dfrac{{3\pi}}{2}$	$2\pi$
$y =\sec2x$	$1$	$1$	$- 1$	$1$	$- 1$	$1$

By using this tabular column we can easily make the following graph,

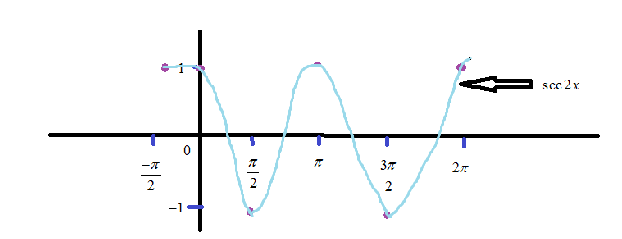
The above graph shows the one cycle of $\sec 2x$

Note: Note that when $\theta$ is the end with $\dfrac{\pi }{2}$ the term, all $\cos \theta$ value becomes zero. Also, note that when $\theta$ has an odd $\pi$ term, all the $\cos \theta$ values become $- 1$ and when $\theta$ has an even $\pi$ term, all the $\cos \theta$ values become $1$. Note that when the denominator value becomes zero, then the answer becomes undefined. This question involves the operation of addition / subtraction/ multiplication/ division. Also, note that $\cos \theta$ is the inverse value of $\sec \theta$. Remember the trigonometric table values to make easy calculations.