Question

How do you simplify the expression $\sin \left( {\arctan x} \right)$ ?

Answer 1

Hint : In order to simplify the expression $\sin \left( {\arctan x} \right)$ , we know that $\arctan x$ is an angle whose tangent function is equal to $\dfrac{x}{1}$ . Take an example of a right angled triangle, with any random angle given, find the value of sides, then through that find the trigonometric values, then put it in $\sin \left( {\arctan x} \right)$ .

Complete step by step solution:
Let’s take a triangle with sides $a,b,c$ with an angle $p$ opposite the perpendicular, which is represented as:

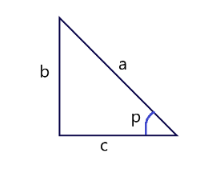
Let $p = \arctan x$
So, we can write it as:
$\tan p = \tan \left( {\arctan x} \right)$
From the basic formulas of trigonometry we know that:
$\tan p = \dfrac{{perpendicular}}{{base}} = \dfrac{b}{c}$
As we know that $\arctan x$ is an angle whose tangent function is equal to $\dfrac{x}{1}$ .
So, from the previous equation we can write:
$\tan p = \tan \left( {\arctan x} \right) = \dfrac{b}{c} = \dfrac{x}{1}$
This implies that perpendicular $\left( b \right) = x$ and base $\left( c \right) = 1$
We need to find the value of $a$ , for that we will use Pythagoras theorem and we get:

$${\left( b \right)^2} + {\left( c \right)^2} = {\left( a \right)^2} \\\ {\left( x \right)^2} + {\left( 1 \right)^2} = {\left( a \right)^2} \\\ {x^2} + 1 = {a^2} \\\ a = \sqrt {{x^2} + 1} \;$$

That implies hypotenuse is equal to $\sqrt {{x^2} + 1}$ .
According to this the new triangle diagram is:

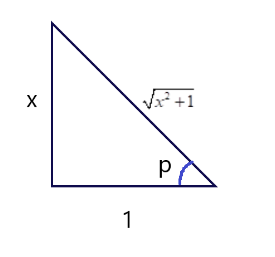
From the basic formulas of trigonometry we know that:
$\sin p = \dfrac{{perpendicular}}{{hypotenuse}} = \dfrac{b}{a}$
Since we wrote $\tan p = \tan \left( {\arctan x} \right) = \dfrac{b}{c} = \dfrac{x}{1}$ , so we can also write this for sine and we get:
$\sin p = \sin \left( {\arctan x} \right) = \dfrac{b}{a} = \dfrac{x}{{\sqrt {{x^2} + 1} }}$
Therefore, the value of $\sin \left( {\arctan x} \right) = \dfrac{x}{{\sqrt {{x^2} + 1} }}$ .
So, the correct answer is $\sin \left( {\arctan x} \right) = \dfrac{x}{{\sqrt {{x^2} + 1} }}$ ”.

Note : With this method we can also find the values for cosine, secant and cosecant.
It's important to remember the basic formula of trigonometry and trigonometric identities to solve these kinds of questions.
We could have also solved it directly by taking the value of $\arctan x$ that is $\dfrac{x}{1}$ for tan, placing them in the triangle finding for the hypotenuse and placing it in the value of sine.