Question

How do you simplify $\tan {{25}^{\circ }}\cot {{25}^{\circ }}$?

Answer 1

Assume the given expression as ‘E’. Consider a right-angle triangle and assume any one of the two acute angles as $\theta$. Consider the trigonometric ratio $\tan \theta$ and $\cot \theta$ assuming the side opposite to the angle $\theta$ as the perpendicular, the other side as the base and the side opposite to the angle ${{90}^{\circ }}$ as the hypotenuse. Find the value of $\tan \theta \times \cot \theta$ and use it to get the value of the provided expression.

Complete step by step solution:
Here, we have been provided with the expression $\tan {{25}^{\circ }}\cot {{25}^{\circ }}$ and we are asked to simplify it. Let us know the given expression as ‘E’, so we have,
$\Rightarrow E=\tan {{25}^{\circ }}\cot {{25}^{\circ }}$
Since, we don’t know the value of the tangent and cotangent function for the angle ${{25}^{\circ }}$, so we need to use some other approach to get the answer. Let us see if we can derive a formula for the product of the tangent and cotangent function.

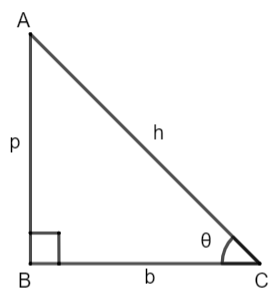
In the above figure we have assumed a right-angled triangle at B. Angle C is considered as $\theta$, so the side AB will be the perpendicular, BC as the base and AC as the hypotenuse. We know that the tangent function is the ratio of perpendicular to the base while cotangent function is the ratio of base to the perpendicular, so mathematically we have,
$\Rightarrow \tan \theta =\dfrac{AB}{BC}=\dfrac{p}{b}$ - (1)
$\Rightarrow \cot \theta =\dfrac{BC}{AB}=\dfrac{b}{p}$ - (2)
Multiplying the above two equations, we get,
$\Rightarrow \tan \theta \times \cot \theta =\dfrac{p}{b}\times \dfrac{b}{p}$
Cancelling the common terms, we get,
$\Rightarrow \tan \theta \times \cot \theta =1$
Therefore, the value of the product of the tangent and cotangent function is always 1 for the same angle, irrespective of the value of $\theta$. So, substituting $\theta ={{25}^{\circ }}$, we get,

& \Rightarrow \tan {{25}^{\circ }}\times \cot {{25}^{\circ }}=1 \\\ & \Rightarrow E=1 \\\ \end{aligned}$$ Hence, the value of the given expression is 1. **Note:** One must remember that in the identity $$\tan \theta .\cot \theta =1$$, $$\theta $$ must not be odd multiple of $$\dfrac{\pi }{2}$$ or multiple of $$\pi $$ because at $$\dfrac{\pi }{2}$$ tangent function is undefined or we can say that its value reaches $$\infty $$ and similarly at $${{0}^{\circ }}$$ the value of cotangent function reaches $$\infty $$ and we know that $$\infty $$ is not a real number. So, we must not consider such values of $$\theta $$. In addition to the identity, $$\tan \theta .\cot \theta =1$$ you must also remember the identities: - $$\sec \theta .\cos \theta =1$$ and $$\sin \theta .\csc \theta =1$$.