Question

How do you simplify $\sin x\sec x$?

Answer 1

Here, we will assume the angle $x$ to be the interior angle of a right angled triangle. We will express the trigonometric ratios in terms of sides of the right angled triangle. Then we will simplify the given expression by multiplying the terms to get the required answer.

Complete step-by-step answer:
Let angle $x$ be the interior angle of a right angled triangle with P as perpendicular, B as base, and H as hypotenuse.
The sine of an angle of a right angled triangle is the ratio of its perpendicular and hypotenuse.
Therefore, we get
$\sin x = \dfrac{P}{H}$

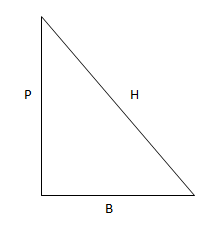
The secant of an angle of a right angled triangle is the ratio of its hypotenuse and base.
Therefore, we get
$\sec x = \dfrac{H}{B}$
Substituting $\sin x = \dfrac{P}{H}$ and $\sec x = \dfrac{H}{B}$ in the given expression, we get
$\sin x\sec x = \dfrac{P}{H} \times \dfrac{H}{B}$
Simplifying the expression, we get
$\Rightarrow \sin x\sec x = \dfrac{P}{B}$
The tangent of an angle of a right angled triangle is the ratio of its perpendicular and base.
Therefore, we get
$\tan x = \dfrac{P}{B}$
Substituting $\dfrac{P}{B} = \tan x$ in the equation $\sin x\sec x = \dfrac{P}{B}$, we get
$\Rightarrow \sin x\sec x = \tan x$
Therefore, we have simplified the expression $\sin x\sec x$ as $\tan x$.

Note: We can also convert the trigonometric ratio of secant to cosine, and then the quotient of sine and cosine to tangent to simplify the given expression.
The secant of an angle $x$ can be written as the reciprocal of cosine of the angle $x$. This can be written as $\sec x = \dfrac{1}{{\cos x}}$.
Substituting $\sec x = \dfrac{1}{{\cos x}}$ in the given expression, we get
$\Rightarrow \sin x\sec x = \sin x \times \dfrac{1}{{\cos x}}$
Rewriting the expression, we get
$\Rightarrow \sin x\sec x = \dfrac{{\sin x}}{{\cos x}}$
The secant of an angle $x$ can be written as the quotient of the sine and cosine of the angle $x$. This can be written as $\tan x = \dfrac{{\sin x}}{{\cos x}}$.
Substituting $\dfrac{{\sin x}}{{\cos x}} = \tan x$ in the equation $\sin x\sec x = \dfrac{{\sin x}}{{\cos x}}$, we get
$\Rightarrow \sin x\sec x = \tan x$
Therefore, we have simplified the expression $\sin x\sec x$ as $\tan x$.