Question

How do you simplify $\sec (\arctan (4x))$?

Answer 1

We will consider the inner function as an angle. Then we will eliminate the function $\arctan$ from the resulting expression. Next, we will draw a right triangle based on the expression. Finally, we will find $\sec$ of the angle we have considered.

Formula used:
$\tan (\arctan (x)) = x$

Complete step by step solution:
We are required to simplify the expression $\sec (\arctan (4x))$.
Let us begin by denoting the innermost function, which is $\arctan (4x)$ as an angle $\theta$. We get
$\theta = \arctan (4x)$ ………$(1)$
Let us try to eliminate the function $\arctan$ from equation $(1)$ by taking $\tan$ on both sides of equation $(1)$. This gives us
$\tan \theta = \tan (\arctan (4x))$ ………..$(2)$
We will use the property $\tan (\arctan (x)) = x$ on the RHS of equation $(2)$ to get the following expression:
$\tan \theta = 4x$ ………$(3)$
Let us consider a right triangle ABC with right-angle $\angle B$ as in the figure. Let us take $\theta$ as the angle between the sides $AC$ and $BC$.

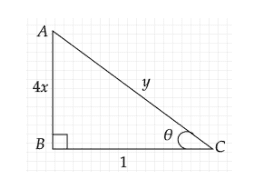
Now, from equation $(3)$, we can write
$\tan \theta = \dfrac{{4x}}{1}$
We know that in a right-triangle ABC,
$\tan \theta = \dfrac{{{\rm{opp}}{\rm{. side}}}}{{{\rm{adj}}{\rm{. side}}}}$. Compared with the above equation, we can take the opposite side of the right-triangle as $4x$ units and the adjacent side as $1$ unit.
Now, we have to find the hypotenuse of the right triangle with sides $4x$ units and $1$ units.
By Pythagoras theorem, we have $A{C^2} = A{B^2} + B{C^2}$. Substituting $AC = y,AB = 4x$ and $BC = 1$, we get
${y^2} = {(4x)^2} + {1^2}$
Taking square root on both sides of the above expression, we get
$y = \sqrt {16{x^2} + 1}$ ……..$(4)$
We are supposed to find the value of $\sec (\arctan (4x))$, which from equation $(1)$ is the same as $\sec \theta$.
We know that $\sec \theta = \dfrac{{{\rm{hypotenuse}}}}{{{\rm{adj}}{\rm{. side}}}}$. So, from triangle ABC and equation $(4)$, we get
$\sec \theta = \dfrac{{\sqrt {16{x^2} + 1} }}{1} = \sqrt {16{x^2} + 1}$

Note:
The functions $\tan$ and $\arctan$ are inverse functions. We have used the property $\tan (\arctan (x)) = x$ to eliminate the function $\arctan$, since we cannot use that function in a right-angled triangle. Similarly, we have properties $\sin (\arcsin (x)) = x$ and $\cos (\arccos (x)) = x$.