Question

How do you simplify $\csc \theta \sin \theta$ $?$

Answer 1

Hint : The question is related to trigonometry, the sine, cosine, tangent, cosecant, secant, cotangent are trigonometry ratios and this can be abbreviated as sin, cos, tan, csc or cosec, sec, cot by using the definition of trigonometric ratios of the right-angled triangle we can simplify the given question.

Complete step-by-step answer :
Trigonometric ratios: Some ratios of the sides of a right-angle triangle with respect to its acute angle called trigonometric ratios of the angle.

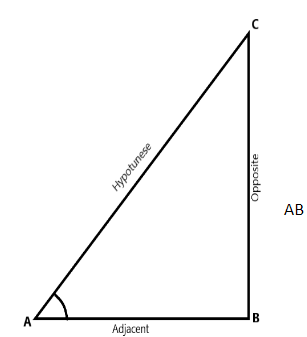
Let us consider the triangle ABC here $\left| \\!{\underline {\, {CAB} \,}} \right.$ is an acute angle. BC is the opposite to the angle A and AB is the adjacent to the angle A. So, we call BC as opposite side and AB is adjacent side and AC is hypotenuse.
The trigonometric ratios of angle A in the given right angled triangle are defined as.
Sine of $\left| \\!{\underline {\, A \,}} \right. = \dfrac{{Opposite\,side\,of\,\left| \\!{\underline {\, A \,}} \right. }}{{hypotenuse}} = \dfrac{{BC}}{{AC}}$
Cosine of $\left| \\!{\underline {\, A \,}} \right. = \dfrac{{Adjacent\,side\,of\,\left| \\!{\underline {\, A \,}} \right. }}{{hypotenuse}} = \dfrac{{AB}}{{AC}}$
Tangent of $\left| \\!{\underline {\, A \,}} \right. = \dfrac{{Opposite\,side\,of\,\left| \\!{\underline {\, A \,}} \right. }}{{Adjacent\,side\,of\,\left| \\!{\underline {\, A \,}} \right. }} = \dfrac{{BC}}{{AB}}$
Cosecant of $\left| \\!{\underline {\, A \,}} \right. = \dfrac{{hypotenuse}}{{Opposite\,side\,of\,\left| \\!{\underline {\, A \,}} \right. }} = \dfrac{{AC}}{{BC}}$
Secant of $\left| \\!{\underline {\, A \,}} \right. = \dfrac{{hypotenuse}}{{Adjacent\,side\,of\,\left| \\!{\underline {\, A \,}} \right. }} = \dfrac{{AC}}{{AB}}$
Cotangent of $\left| \\!{\underline {\, A \,}} \right. = \dfrac{{Adjacent\,side\,of\,\left| \\!{\underline {\, A \,}} \right. }}{{Opposite\,\,side\,of\,\left| \\!{\underline {\, A \,}} \right. }} = \dfrac{{AB}}{{BC}}$
The ratios defined are abbreviated as sin A, cos A, tan A, csc A or cosec A, sec A and cot A
Cosecant A also can be defined as reciprocal of sine A i.e., $\csc A = \dfrac{1}{{\sin A}}$
secant A also can be defined as reciprocal of cosine A i.e., $\sec A = \dfrac{1}{{\cos A}}$
cotangent A also can be defined as reciprocal of tan A i.e., $\cot A = \dfrac{1}{{\tan A}}$
Using these definitions of trigonometric ratios, we can simplify the given question
Consider the $\csc \theta \sin \theta$
As we know already $\csc \,A = \dfrac{1}{{\sin A}}$
$\Rightarrow \,\,\csc \theta \sin \theta = \dfrac{1}{{\sin \theta }}.\sin \theta \\\ \,\,\,\therefore \,\,\csc \theta \sin \theta = 1 \;$
Hence, by simplifying we get $\csc \theta .\sin \theta = 1$
So, the correct answer is “1”.

Note : The trigonometry ratios are interlinked to other trigonometry ratio, if we consider cosecant, secant and cotangent they are interlinked to sine, cosine and tangent of the angle respectively. The trigonometry ratios are defined as ratios of the side of a right-angled triangle with respect to its acute angle.