Question

How do you show that $x + 7$ is a factor of ${x^3} - 37x + 84$ . then factor completely?

Answer 1

In this question, we want to prove whether $x + 7$ is the factor of the given equation. For that equate $x + 7$ to zero which will give $x = - 7$. Put this value in the given equation, if we get zero then $x + 7$ is a factor of the equation. After that divide the equation with $x + 7$ . We will get the quadratic equation which we can easily solve by the factoring method.

Complete step by step solution:
We are provided with the equation ${x^3} - 37x + 84$
Firstly, proving that whether $x + 7$ is a factor of the given equation. For that putting $x = - 7$ in the
given equation.
${\left( { - 7} \right)^3} - 37\left( { - 7} \right) + 84 \\\ = - 343 + 259 + 84 \\\ = - 343 + 343 \\\ = 0 \\\$
Which proves that $x + 7$ is one factor for the given equation.
Now, we have to find the other two factors. For that dividing the ${x^3} - 37x + 84$ by $x + 7$ .

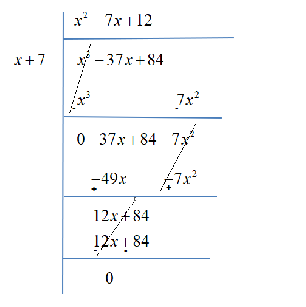
Hence, we now left with a quadratic equation ${x^2} - 7x + 12 = 0$
Finding factors by factoring method,
${x^2} - 3x - 4x + 12 = 0 \\\ x\left( {x - 3} \right) - 4\left( {x - 3} \right) = 0 \\\ \left( {x - 3} \right)\left( {x - 4} \right) = 0 \\\ \left( {x - 3} \right) = 0 \\\ \left( {x - 4} \right) = 0 \\\$
Hence, factors of the above given equation are $- 7,3,4$

Note: Solve the equation carefully. Take care of the signs while dividing the given equation by $x + 7$ . We can also use the formula for solving the quadratic equation. Make sure that the factor is firstly be checked by putting that value of x into the given equation.