Question

How do you show that $f(x) = \dfrac{1}{x}$ and $g(x) = \dfrac{1}{x}$ are inverse functions algebraically and graphically?

Answer 1

According to given in the question we have to determine the inverse functions algebraically and graphically of $f(x) = \dfrac{1}{x}$ and $g(x) = \dfrac{1}{x}$ as mentioned in the question. So, first of all to determine the inverse functions algebraically and graphically we have to replace the values of $f(x)$ and $g(x)$.
Now, we have to solve the expression as obtained after replacing the terms of the expression given and then we have to obtain the value algebraically.
Now, as we know that these are their own inverse we would expect their graphs to be symmetrical about the line which is $y = x.$

Complete step-by-step solution:
Step 1: First of all to determine the inverse functions algebraically and graphically we have to replace the values of $f(x)$ and $g(x)$. Hence,
$\Rightarrow f(g(x)) = g(f(x)) = x$
Step 2: Now, we have to solve the expression as obtained after replacing the terms of the expression given and then we have to obtain the value algebraically. Hence,

$$\Rightarrow \dfrac{1}{{g(x)}} = \dfrac{1}{{f(x)}} = x \\\ \Rightarrow \dfrac{1}{{\dfrac{1}{x}}} = \dfrac{1}{{\dfrac{1}{x}}} = x \\\ \Rightarrow x = x = x$$

Step 3: Now, as we know that these are their own inverse we would expect their graphs to be symmetrical about the line which is $y = x.$ Hence, the graph is mentioned below:

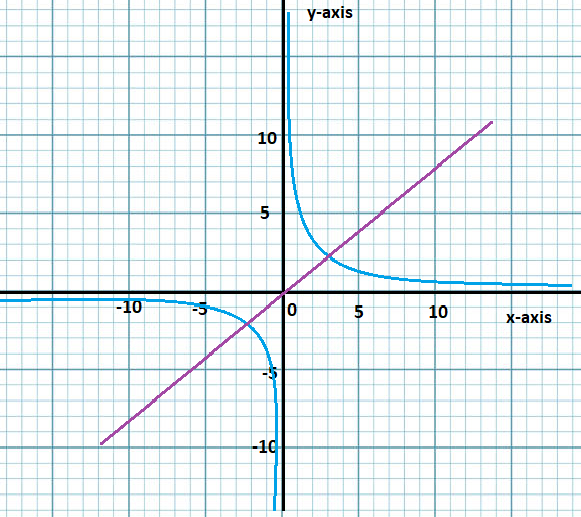
Hence, we have determined the inverse functions algebraically and graphically as $x = x = x$ and the graph is as below:

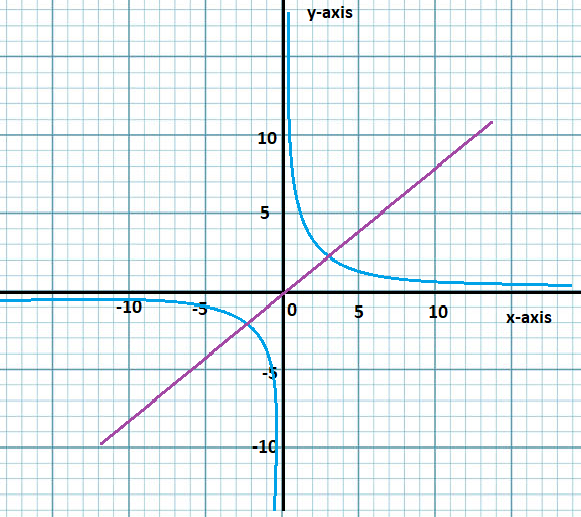
Note: It is necessary that we have to revert the values of $f(x) = \dfrac{1}{x}$ and $g(x) = \dfrac{1}{x}$ to determine the inverse of these functions algebraically.
To represent graphically these are their own inverse we would expect their graphs to be symmetrical about the line which is $y = x.$