Question

How do you show that $1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta$ ?

Answer 1

In this question, we have to show that the equation is true. This question consists of an equation with trigonometric functions, so we will use trigonometric identities and formulas to prove this question. We start solving this problem by using a trigonometric identity ${{\sin }^{2}}x+{{\cos }^{2}}x=1$ , after that we divide both sides of this equation by ${{\cos }^{2}}x$. Then make necessary calculations, and again use the trigonometric formula ${{\tan }^{2}}x=\dfrac{{{\sin }^{2}}x}{{{\cos }^{2}}x}$ and ${{\sec }^{2}}x=\dfrac{1}{{{\cos }^{2}}x}$ in the equation, to get the required equation, which is the answer to our problem.

Complete answer:
According to the question, it is given that there is a trigonometric equation $1+{{\tan }^{2}}\theta ={{\sec }^{2}}\theta$ , in which we have to prove that LHS=RHS.
So, we will apply the trigonometric identities and formulas, to do the same.
Now, we starting solving this problem using a trigonometric identity,
${{\sin }^{2}}x+{{\cos }^{2}}x=1$ --------- (1)
We will divide ${{\cos }^{2}}x$ on both sides of the equation (1), we get
$\Rightarrow \dfrac{{{\sin }^{2}}x+{{\cos }^{2}}x}{{{\cos }^{2}}x}=\dfrac{1}{{{\cos }^{2}}x}$
So, we will split the denominator with respect to addition in the LHS of the above equation, we get
$\Rightarrow \dfrac{{{\sin }^{2}}x}{{{\cos }^{2}}x}+\dfrac{{{\cos }^{2}}x}{{{\cos }^{2}}x}=\dfrac{1}{{{\cos }^{2}}x}$
Also, we know that the same terms will cancel out in division with a quotient 1, therefore we get
$\Rightarrow \dfrac{{{\sin }^{2}}x}{{{\cos }^{2}}x}+1=\dfrac{1}{{{\cos }^{2}}x}$
Now, we will apply the trigonometric formula ${{\tan }^{2}}x=\dfrac{{{\sin }^{2}}x}{{{\cos }^{2}}x}$ in the above equation, we get
$\Rightarrow {{\tan }^{2}}x+1=\dfrac{1}{{{\cos }^{2}}x}$
Again, we will apply the trigonometric formula ${{\sec }^{2}}x=\dfrac{1}{{{\cos }^{2}}x}$ on the right-hand side of the above equation, we get
$\Rightarrow {{\tan }^{2}}x+1={{\sec }^{2}}x$ which is the required equation.
Therefore, we proved that $1+{{\tan }^{2}}x={{\sec }^{2}}x$.

Note: Always do all the steps carefully and do step by step, to avoid confusion and errors. Do mention all the identities and formulas in each step. One of the alternative methods is we can prove this equation using triangular ratios.
An alternative method:
The equation we have to prove is $1+{{\tan }^{2}}x={{\sec }^{2}}x$
Let us start proving this problem using $LHS=1+{{\tan }^{2}}x$ ---------- (2)

First we will draw a right-angled triangle ABC, where BC is the hypotenuse, AC is the perpendicular of the triangle, and AB is the base of the triangle that is

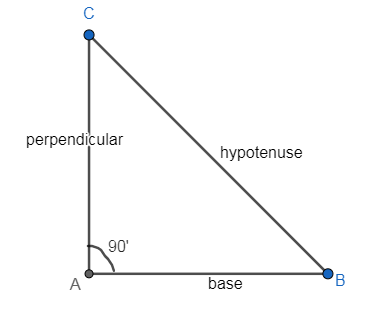
From above graph, we will apply the triangular ratios, as know that all the trigonometric functions can be expressed in the triangular ratios, that is $\tan x=\dfrac{perpendicular}{base}$ , thus we put the trigonometric ratio in equation (2), we get
$\Rightarrow 1+{{\left( \dfrac{perpendicular}{base} \right)}^{2}}$
Now, we take LCM in the above equation, we get
$\Rightarrow \dfrac{{{(base)}^{2}}+{{(perpendicular)}^{2}}}{{{(base)}^{2}}}$
By using Pythagoras theorem ${{(hypotenuse)}^{2}}={{(base)}^{2}}+{{(perpendicular)}^{2}}$ in the above equation, we get
$\Rightarrow \dfrac{{{(hypotenuse)}^{2}}}{{{(base)}^{2}}}$
As we know, the trigonometric ratio $\sec x=\dfrac{hypotenuse}{base}$ , therefore we get
$\Rightarrow {{\sec }^{2}}x=RHS$
Hence proved.