Solveeit Logo
Login

Question

Question: How do you rotate the axes to transform the equation \({x^2} + xy = 3\) into a new equation with no ...

How do you rotate the axes to transform the equation x2+xy=3{x^2} + xy = 3 into a new equation with no xyxy term and then find angle of rotation?

Explanation

Solution

Transforming an equation means rotating the coordinate axes without shifting the origin by an angle θ\theta . The old coordinates can be represented by using new coordinates. Hence, substituting them in the equation given in the question will give us the new equation (after the rotation).
Let (x,y)(x,y) be old coordinates and (x′,y′)(x',y') be the new coordinates.
The relation between them can be given by the formula:
x=x′cos⁡θ−y′sin⁡θx = x'\cos \theta - y'\sin \theta and y=x′sin⁡θ+y′cos⁡θy = x'\sin \theta + y'\cos \theta
Where θ\theta is the angle of rotation of the coordinate axis.

Complete step-by-step answer:
Let’s draw a diagram to represent the rotation of axes.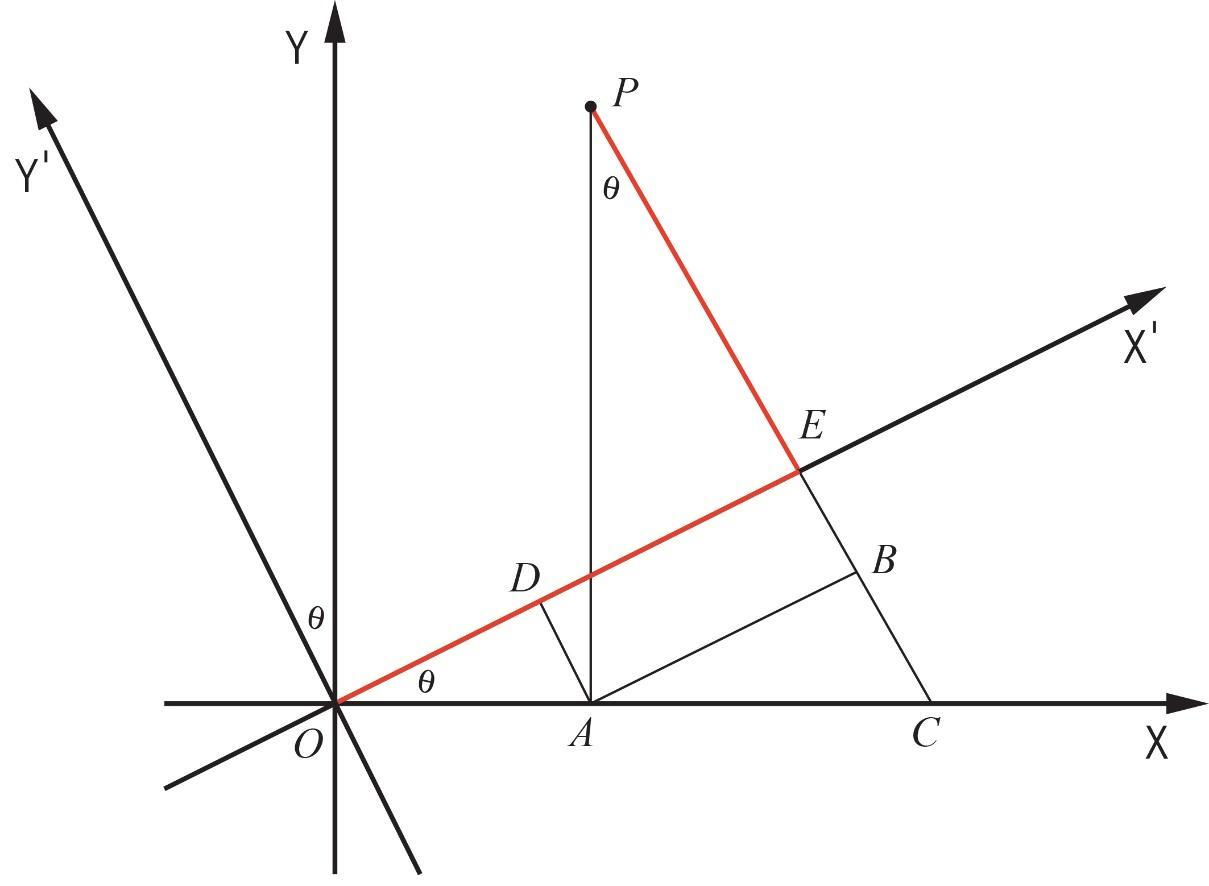
The old equation is x2+xy=3{x^2} + xy = 3
When we substitute above mentioned new coordinates in place of old coordinates, we get:
(x′cos⁡θ−y′sin⁡θ)2+(x′cos⁡θ−y′sin⁡θ)(x′sin⁡θ+y′cos⁡θ)=3{(x'\cos \theta - y'\sin \theta )^2} + (x'\cos \theta - y'\sin \theta )(x'\sin \theta + y'\cos \theta ) = 3
By opening all the brackets, we get:
(x′2cos⁡2θ+y′2sin⁡2θ−2x′y′sin⁡θcos⁡θ)+(x′2cos⁡θsin⁡θ−y′2cos⁡θsin⁡θ+x′y′cos⁡2θ−x′y′sin⁡2θ)=3(x{'^2}{\cos ^2}\theta + y{'^2}{\sin ^2}\theta - 2x'y'\sin \theta \cos \theta ) + (x{'^2}\cos \theta \sin \theta - y{'^2}\cos \theta \sin \theta + x'y'{\cos ^2}\theta - x'y'{\sin ^2}\theta ) = 3
By taking out coefficients of same terms common we get;
x′2(cos⁡2θ+cos⁡θsin⁡θ)+y′2(sin⁡2θ−cos⁡θsin⁡θ)+x′y′(−2cos⁡θsin⁡θ−sin⁡2θ+cos⁡2θ)=3x{'^2}({\cos ^2}\theta + \cos \theta \sin \theta ) + y{'^2}({\sin ^2}\theta - \cos \theta \sin \theta ) + x'y'( - 2\cos \theta \sin \theta - {\sin ^2}\theta + {\cos ^2}\theta ) = 3
In the question we are asked to eliminate the xyxy term, so we have to make the coefficient of xyxy term zero. By doing so we get;
−2cos⁡θsin⁡θ−sin⁡2θ+cos⁡2θ=0- 2\cos \theta \sin \theta - {\sin ^2}\theta + {\cos ^2}\theta = 0
2cos⁡θsin⁡θ=−sin⁡2θ+cos⁡2θ2\cos \theta \sin \theta = - {\sin ^2}\theta + {\cos ^2}\theta
We know the basic trigonometric formulae:
sin⁡2θ=2cos⁡θsin⁡θ\sin 2\theta = 2\cos \theta \sin \theta
cos⁡2θ=−sin⁡2θ+cos⁡2θ\cos 2\theta = - {\sin ^2}\theta + {\cos ^2}\theta
By substituting the above formulae we get:
sin⁡2θ=cos⁡2θ\sin 2\theta = \cos 2\theta
tan⁡2θ=1\tan 2\theta = 1
By using inverse trigonometric formula of tan, we get:
2θ=nπ+π42\theta = n\pi + \dfrac{\pi }{4}
θ=nπ2+π8\theta = \dfrac{{n\pi }}{2} + \dfrac{\pi }{8} where n can be any integer.
Hence, we can have more than one answer by taking different values of n.
Let’s take n value as zero, we get:
x′2(cos⁡222.5∘+cos⁡22.5∘sin⁡22.5∘)+y′2(sin⁡222.5∘−cos⁡22.5∘sin⁡22.5∘)=3x{'^2}({\cos ^2}22.5^\circ + \cos 22.5^\circ \sin 22.5^\circ ) + y{'^2}({\sin ^2}22.5^\circ - \cos 22.5^\circ \sin 22.5^\circ ) = 3
We know that:
cos⁡22.5∘=0.92\cos 22.5^\circ = 0.92
sin⁡22.5∘=0.38\sin 22.5^\circ = 0.38
By substituting the corresponding values, we get:
x′2(1.196)+y′2(−0.2052)=3x{'^2}\left( {1.196} \right) + y{'^2}( - 0.2052) = 3

Note: The above given equation is only one of the possible answers. There can be more than one solution by taking different values of n. We need to be careful while using the formulae and remembering the basic trigonometric formulae will always come in handy since they make the calculation a lot easier. When finding the new equation, there is a lot of calculation involved so one should be careful while doing the mathematics involved. The formula can be derived from basic congruence of the triangles.