Question

How do you rotate the axes to transform the equation $xy+4=0$ into a new equation with no $xy$ term and then find the angle of rotation?

Answer 1

We must first write the equations for the transformation of the coordinate system. Using the equations, we must eliminate the term $xy$ from the resulting new equation. We must accordingly find the angle of rotation $\theta$ . Using this value of the angle of rotation, we can find the desired equation for the rotated coordinate system.

Complete step-by-step solution:
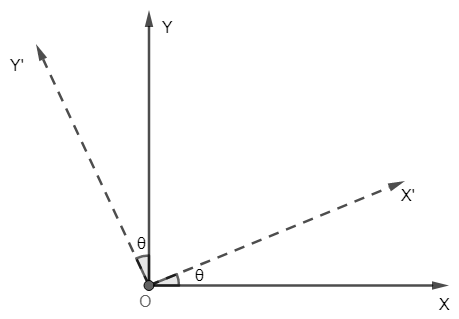
We have the coordinate system with X and Y axes, and we are rotating the whole coordinate system by an angle, say $\theta$ , in the anticlockwise direction. If by our calculation, $\theta$ comes out to be negative, then we will know that the rotation is in clockwise direction.
Let X’ and Y’ be the new coordinate axes after rotation.

Let $i\text{ and }j$ be the unit vectors in the direction of X-axis and Y-axis respectively, and $i'\text{ and }j'$ be the unit vectors along the X’-axis and Y’-axis respectively. So, now we have

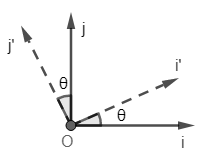
From the above figure, we can easily write unit vectors $i'\text{ and }j'$ in terms of $i\text{ and }j$ vectors.
$\begin{aligned} & i'=i\cos \theta +j\sin \theta \\\ & j'=-i\sin \theta +j\cos \theta \\\ \end{aligned}$
Let us assume a vector in the original coordinate system,
$v=xi+yj...\left( i \right)$
Now, in the new coordinate system, we can write the same vector as
$v=x'i'+y'j'$
Putting the values of $i'\text{ and }j'$ , we get
$v=x'\left( i\cos \theta +j\sin \theta \right)+y'\left( -i\sin \theta +j\cos \theta \right)$
$\Rightarrow v=ix'\cos \theta +jx'\sin \theta -iy'\sin \theta +jy'\cos \theta$
$\Rightarrow v=ix'\cos \theta -iy'\sin \theta +jx'\sin \theta +jy'\cos \theta$
$\Rightarrow v=\left( x'\cos \theta -y'\sin \theta \right)i+\left( x'\sin \theta +y'\cos \theta \right)j...\left( ii \right)$
Comparing equation (i) and equation (ii), as both of them represent the same point, we get
$\begin{aligned} & x=x'\cos \theta -y'\sin \theta ...\left( iii \right) \\\ & y=x'\sin \theta +y'\cos \theta ...\left( iv \right) \\\ \end{aligned}$
Thus, we have derived the equation for transformation of axes.
We have to transform the equation $xy+4=0$ .
Putting the values from equation (iii) and (iv), we get
$\left( x'\cos \theta -y'\sin \theta \right)\left( x'\sin \theta +y'\cos \theta \right)+4=0$
Multiplying the above, we get
$x{{'}^{2}}\sin \theta \cos \theta +x'y'{{\cos }^{2}}\theta -x'y'{{\sin }^{2}}\theta -y{{'}^{2}}\sin \theta \cos \theta +4=0$
$\Rightarrow \left( x{{'}^{2}}-y{{'}^{2}} \right)\sin \theta \cos \theta +x'y'\left( {{\cos }^{2}}\theta -{{\sin }^{2}}\theta \right)+4=0...\left( v \right)$
We are given in the question that the term $xy$ must not be present.
So, we can clearly say that
${{\cos }^{2}}\theta -{{\sin }^{2}}\theta =0$
Or, we can say that
$\cos 2\theta =0$
We know that for $\cos \phi =0,\text{ }\phi =\left( 2n+1 \right)\dfrac{\pi }{2}$ , where n is integer.
So, for $\cos 2\theta =0,\text{ 2}\theta =\left( 2n+1 \right)\dfrac{\pi }{2}$ .
Or, $\theta =\left( 2n+1 \right)\dfrac{\pi }{4}$
For $n=0$ , we have $\theta =\dfrac{\pi }{4}$
Putting $\theta =\dfrac{\pi }{4}$ in equation (v), we get

& \left( x{{'}^{2}}-y{{'}^{2}} \right)\left( \dfrac{1}{\sqrt{2}}\times \dfrac{1}{\sqrt{2}} \right)+x'y'\left( \dfrac{1}{2}-\dfrac{1}{2} \right)+4=0 \\\ & \Rightarrow \dfrac{1}{2}\left( x{{'}^{2}}-y{{'}^{2}} \right)+0+4=0 \\\ & \Rightarrow \dfrac{1}{2}\left( x{{'}^{2}}-y{{'}^{2}} \right)=-4 \\\ & \Rightarrow x{{'}^{2}}-y{{'}^{2}}+8=0 \\\ \end{aligned}$$ **Hence, the equation $xy+4=0$ in the rotated coordinate system is $$x{{'}^{2}}-y{{'}^{2}}+8=0$$ , and the angle of rotation is $\theta =\dfrac{\pi }{4}$ radians or $\theta ={{45}^{\circ }}$.** **Note:** We must remember that the above solution is just one of the possible answers. We can get another equation for different values of n. For example, for $n=1$ , the equation will be $$x{{'}^{2}}-y{{'}^{2}}-8=0$$ . Hence, the complete set of equations is $$x{{'}^{2}}-y{{'}^{2}}=\pm 8$$ .