Question

How do you put the equation $2y - 3x = 5$ into slope-intercept form, and graph the equation?

Answer 1

We shift all constant values to the opposite side as that of y and then divide the equation on both sides with such a number such that we get only y on one side of the equation and rest values on the other side of the equation.

• General equation of line in slope-intercept form is $y = mx + c$ where m is the slope of the line and c is the y-intercept.
• Intercept means the point where the line crosses the respective axis.

Complete step-by-step answer:
We have equation of line $2y - 3x = 5$ … (1)
We write the equation similar to the general equation of line i.e. in such a way that ‘y’ comes at one side of the equation.
Shift all values except 2y to right hand side of the equation
$\Rightarrow 2y = 3x + 5$
Now we see that the number which has to be removed from left hand side of the equation to make left hand side of the equation only as ‘y’ is 2, so we divide both sides of the equation by this number i.e. 2
Divide both sides of the equation by 2
$\Rightarrow \dfrac{{2y}}{2} = \dfrac{{3x + 5}}{2}$
Cancel same factors from numerator and denominator on both sides of the equation
$\Rightarrow y = \dfrac{3}{2}x + \dfrac{5}{2}$
So this equation of line matches the general form of slope-intercept form.
$\therefore$Slope-intercept form of the equation $2y - 3x = 5$ is $y = \dfrac{3}{2}x + \dfrac{5}{2}$
Compare this to general slope-intercept form $y = mx + c$
We get $m = \dfrac{3}{2};c = \dfrac{5}{2}$
So, the slope of line is $\dfrac{3}{2}$ and y-intercept is $\dfrac{5}{2}$
Since y-intercept means x-coordinate is 0, we will write the value of y when x is 0 as $\dfrac{5}{2}$
So, the point becomes $\left( {0,\dfrac{5}{2}} \right)$
Now we calculate the x-intercept of the line.
Since we know x-intercept means that line cuts the x-axis so y coordinate of this point will be 0
Put $y = 0$in $y = \dfrac{3}{2}x + \dfrac{5}{2}$
$\Rightarrow 0 = \dfrac{3}{2}x + \dfrac{5}{2}$
Shift constant values to left hand side of the equation
$\Rightarrow - \dfrac{5}{2} = \dfrac{3}{2}x$
Cancel same factors from denominators of both sides of the equation
$\Rightarrow 3x = - 5$
Cross multiply 3 from left hand side to right hand side of the equation
$\Rightarrow x = \dfrac{{ - 5}}{3}$
So, the point becomes $\left( {\dfrac{{ - 5}}{3},0} \right)$
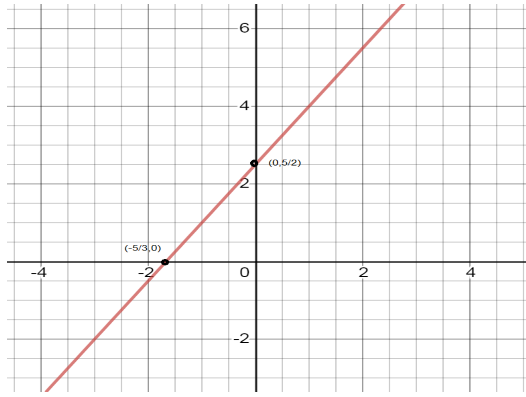
Now we plot the points of x and y intercepts on the graph i.e. plot $\left( {0,\dfrac{5}{2}} \right)$ and $\left( {\dfrac{{ - 5}}{3},0} \right)$ on graph.
Join the points to form the line $2y - 3x = 5$

Note:
Students are likely to make mistakes while shifting the values from one side of the equation to another side of the equation as they forget to change the sign of the value shifted. Keep in mind we always change the sign of the value from positive to negative and vice versa when shifting values from one side of the equation to another side of the equation. Also, when comparing the equation to the general equation, always keep in mind the sign of the slope and y-intercept should be taken along the value, many students tend to make the mistake of writing only the value and forget the sign.