Question

How do you prove $\tan \theta \cot \theta =1$?

Answer 1

To prove this $\tan \theta \cot \theta =1$, we will use a right-angled triangle with one angle $\theta$. In the right angle triangle, we will find the values of $\tan \theta$ and $\cot \theta$ with the help of $\sin \theta$ and $\cos \theta$. And then we will simplify it to get the required statement.

Complete step-by-step solution:
In this question, we have been asked to prove that $\tan \theta \cot \theta =1$.
For that, let us take a right angle triangle ABC.

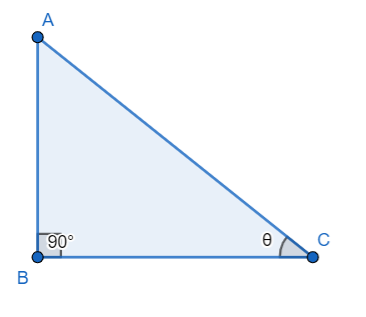
In the above right angle triangle ABC, we have considered the right angle at B and $\angle C=\theta$.
So we can say, AB is the perpendicular, BC is the base and AC is the hypotenuse of the right-angled triangle ABC.
Now, we will try to find or calculate $\sin \theta$.
In the right angle triangle ABC,
As we know that $\sin \theta$ is the ratio of the perpendicular to the hypotenuse.
We can mathematically represent it as $\sin \theta =\dfrac{AB}{AC}$………(1)
Now, we will try to find or calculate $\cos \theta$.
In the right angle triangle ABC,
As we know that $\cos \theta$ is the ratio of the base to the hypotenuse.
We can mathematically represent it as $\cos \theta =\dfrac{BC}{AC}$………..(2)
Now, we will try to find or calculate $\tan \theta$.
In the right angle triangle ABC,
As we know that $\tan \theta$ is the ratio of $\sin \theta$ to $\cos \theta$.
We can mathematically represent it as $\tan \theta =\dfrac{\sin \theta }{\cos \theta }$……….(3)
Now, we will try to find or calculate $\cot \theta$.
In the right angle triangle ABC,
As we know that $\cot \theta$ is the ratio of $\cos \theta$ to $\sin \theta$.
We can mathematically represent it as $\cot \theta =\dfrac{\cos \theta }{\sin \theta }$………….(4)
Now, we will divide equation (1) by equation (2).
$\Rightarrow \dfrac{\sin \theta }{\cos \theta }=\dfrac{\left( \dfrac{AB}{AC} \right)}{\left( \dfrac{BC}{AC} \right)}$
And we know that the same terms from numerator and denominator cancel out. Therefore, we get
$\Rightarrow \dfrac{\sin \theta }{\cos \theta }=\dfrac{AB}{BC}$
From equation (3), we can write
$\tan \theta =\dfrac{AB}{BC}$……….(5)
Now, we will take the reciprocal of equation (5).
$\Rightarrow \dfrac{1}{\dfrac{\sin \theta }{\cos \theta }}=\dfrac{1}{\dfrac{AB}{BC}}$
$\Rightarrow \dfrac{\cos \theta }{\sin \theta }=\dfrac{BC}{AB}$
But from equation (4), we can say
$\cot \theta =\dfrac{BC}{AB}$……………(6)
Now, we will multiply equation (5) by (6).
$\Rightarrow \tan \theta \cdot \cot \theta =\dfrac{AB}{BC}\cdot \dfrac{BC}{AB}$
And we can further simplify it as
$\Rightarrow \tan \theta \cdot \cot \theta =1$
Hence, we have proved that $\tan \theta \cdot \cot \theta =1$

Note: Whenever we get this type of problem, we will try to use the right angle triangle and then use trigonometry. We can also do this problem in one step because $\tan \theta$ is the reciprocal of $\cot \theta$. Also, we need to keep this property in our mind because we might require this property for other questions.