Question

How do you prove $\tan ( - a) = \tan ({360^o} - a) = - \tan (a)$ ?

Answer 1

In a unit circle, when we move anti-clockwise we get a positive angle and when we move clockwise we get a negative angle. Tangent or $\tan$ of an angle $\theta$ is given by $\tan \theta = \dfrac{{perpendicular}}{{base}}$ which in terms of trigonometric ratios we can write as $\tan \theta = \dfrac{{\sin \theta }}{{\cos \theta }}$. We will observe the unit circle for values and signs of $\tan$ in various quadrants to arrive at the conclusion.

Complete step by step answer:
To understand the behavior of $\tan$ for negative angles we draw a unit circle.

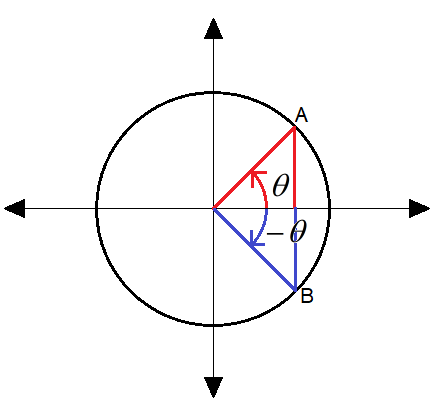
We can see from above diagram that,
For point B, from clockwise we can write the angle as $- \theta$, but from anti-clockwise we can write the same angle as $({360^o} - \theta )$. The value and sign of $\tan$of both angles $- \theta$ and $({360^o} - \theta )$ would be same as we are dealing with the same angles, i.e. we can write,
$\tan ( - \theta ) = \tan ({360^o} - \theta )$
Further,
for point A in quadrant 1 with angle $\theta$, $\tan \theta$ is positive as both perpendicular and base is positive,
and for point B in the quadrant 4 with angle $- \theta$ from clockwise, $\tan ( - \theta )$ is negative as base is positive but perpendicular is negative.
We can make a table with further observation:

When $\theta$ lies in quadrant 1	$- \theta$ lies in quadrant 4	$\tan \theta$ is positive	$\tan ( - \theta )$is negative
When $\theta$ lies in quadrant 2	$- \theta$ lies in quadrant 3	$\tan \theta$ is negative	$\tan ( - \theta )$is positive
When $\theta$ lies in quadrant 3	$- \theta$ lies in quadrant 2	$\tan \theta$ is positive	$\tan ( - \theta )$is negative
When $\theta$ lies in quadrant 4	$- \theta$ lies in quadrant 1	$\tan \theta$ is negative	$\tan ( - \theta )$is positive

Thus, we see from the above table that the sign of $\tan ( - \theta )$ is always opposite to that of $\tan \theta$. But the value will be the same as the value of perpendicular and base would be the same.
So we can write,
$\tan ( - \theta ) = \tan \theta$ but with opposite sign, or
$\tan ( - \theta ) = - \tan \theta$
Thus, we get $\tan ( - \theta ) = \tan ({360^o} - \theta )$ and $\tan ( - \theta ) = - \tan \theta$.
Hence, for any angle $a$ we can write $\tan ( - a) = \tan ({360^o} - a) = - \tan (a)$.

Note: The sign of the perpendicular and base is positive or negative depending on the side of axis it lies on. The value of $\tan \theta$ and $\tan ( - \theta )$ is the same, only the sign is opposite, i.e. when $\tan \theta$ is positive $\tan ( - \theta )$ is negative, and vice-versa. As we wrote $- \theta$ as $({360^o} - \theta )$ from anti-clockwise, we can also write $\theta$ as $- ({360^o} - \theta )$ from clockwise direction. We will get $\tan \theta = \tan ( - ({360^o} - \theta )) = \tan (\theta - {360^o})$.