Question

How do you prove $\csc x=\sec \left( \dfrac{\pi }{2}-x \right)$?

Answer 1

In this question, first we will prove that $\sin x=\cos \left( \dfrac{\pi }{2}-x \right)$. After that, we prove $\csc x=\sec \left( \dfrac{\pi }{2}-x \right)$. For a right angled triangle, $\sin x=\dfrac{opposite}{hypotenuse}$ and $\cos x=\dfrac{adjacent}{hypotenuse}$.
We are going to use these formulas in solving the question.

Complete step by step answer:
Let us solve the question.

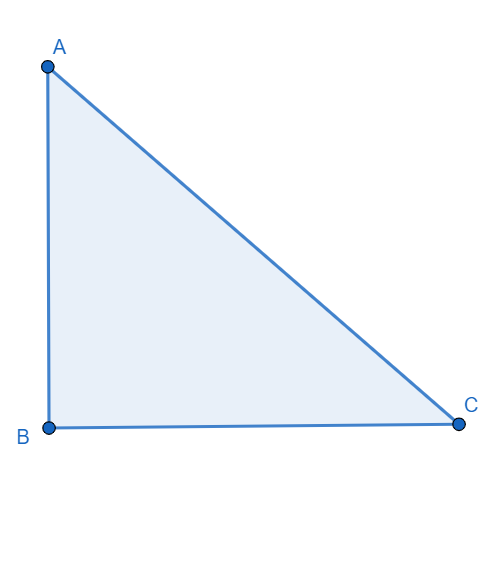
In the given figure, a $\Delta ABC$ is drawn which is a right angled triangle.
In this triangle, AB is perpendicular, BC is base and AC is hypotenuse.
Where $\angle ABC=90{}^\circ$ and let $\angle BAC=x$, then $\angle BCA=\dfrac{\pi }{2}-x$.
Now,
$\cos \angle BCA=\dfrac{adjacent}{hypotenuse}$
$\Rightarrow \cos \left( \dfrac{\pi }{2}-x \right)=\dfrac{BC}{AC}................(1)$
And, $\sin \angle BAC=\dfrac{opoposite}{hypotenuse}$
$\Rightarrow \sin x=\dfrac{BC}{AC}...............(2)$
From the equations (1) and (2), we can say that
$\sin x=\cos \left( \dfrac{\pi }{2}-x \right)$
The above equation can also be written as
$\Rightarrow \dfrac{1}{\sin x}=\dfrac{1}{\cos \left( \dfrac{\pi }{2}-x \right)}$
As we know that $\csc \theta$ is the inverse of $\sin \theta$ and $\sec \theta$ is the inverse of $\cos \theta$.
Hence, the above equation can be written as
$\Rightarrow \csc \theta =\sec \left( \dfrac{\pi }{2}-x \right)$

Note: For this type of question, we should know that the trigonometric functions sin, cos, and tan are inverse of csc, sec, and cot respectively. We can solve this question very easily if we know that $\sin x=\cos \left( \dfrac{\pi }{2}-x \right)$. We just have to inverse both sides, then we will get the answer.
There is another method to solve this question.
Let us prove this question by reverse.
We have to prove $\csc x=\sec \left( \dfrac{\pi }{2}-x \right)$. So, we start from here and make them equal. This will be the reverse process.
$\csc x=\sec \left( \dfrac{\pi }{2}-x \right)$
$\Rightarrow \dfrac{1}{\sin x}=\dfrac{1}{\cos \left( \dfrac{\pi }{2}-x \right)}$
Taking inverse on both sides, we get
$\Rightarrow \sin x=\cos \left( \dfrac{\pi }{2}-x \right)$
We know that cos(X-Y)=cosXcosY-sinXsinY
Using this formula in the above equation, we get
$\Rightarrow \sin x=\cos \left( \dfrac{\pi }{2}-x \right)=\cos \dfrac{\pi }{2}\cos (-x)-\sin \dfrac{\pi }{2}\sin (-x)$
Further solving, we get
$\Rightarrow \sin x=0\times \cos (-x)-1\times \sin (-x)$
$\Rightarrow \sin x=-\sin (-x)$
As we know that, $sin\left( -x \right)=-sinx$
Hence, $sinx=sinx$
Now, it is proved by reverse also.
Therefore, we can use this method also to solve this question.