Question

How do you prove $1 + {\cot ^2}x = \cos e{c^2}x$ ?

Answer 1

Hint : The given equation $1 + {\cot ^2}x = \cos e{c^2}x$ is a famous trigonometric identity. To prove this, we will use some relations. Take the LHS of the equation and try to prove $LHS = RHS$ . Now, we know that $\cot x = \dfrac{{\cos x}}{{\sin x}}$ , so put this in LHS of the given equation and simplify the equation and we will get $LHS = RHS$ .

Complete step-by-step answer :
In this question, we are given a famous trigonometric identity and we need to prove it if its correct.
The given identity is: $1 + {\cot ^2}x = \cos e{c^2}x$ - - - - - - - - - - (1)
Here on the LHS we have $1 + {\cot ^2}x$ and on the RHS we have $\cos e{c^2}x$ . And we need to prove that LHS is equal to RHS that is LHS=RHS.
Now, to prove this we need to use some trigonometric relations or formulas that can be applicable here.
First of all, let us take the LHS of equation (1).
$\to LHS = 1 + {\cot ^2}x$
Now, we know that cot is the ratio of cosine and sine. So, we can write cot is divided by sin.
$\to \cot x = \dfrac{{\cos x}}{{\sin x}} \\\ \to {\cot ^2}x = \dfrac{{{{\cos }^2}x}}{{{{\sin }^2}x}} \;$
So, let us put this value in the LHS of equation (1). Therefore,
$\to LHS = 1 + {\cot ^2}x$
$= 1 + \dfrac{{{{\cos }^2}x}}{{{{\sin }^2}x}}$
Taking L.C.M, we get
$\to LHS = \dfrac{{{{\sin }^2}x + {{\cos }^2}x}}{{{{\sin }^2}x}}$
Now, we know that ${\sin ^2}x + {\cos ^2}x = 1$ . Therefore,
$\to LHS = \dfrac{1}{{{{\sin }^2}x}}$
Now, we know that the inverse of sine is cosecant. Hence, we can write 1 divided by sine as cosec.
$\to \dfrac{1}{{\sin x}} = \cos ecx \\\ \to \dfrac{1}{{{{\sin }^2}x}} = \cos e{c^2}x \;$
Therefore, LHS will become
$\to LHS = \dfrac{1}{{{{\sin }^2}x}} = \cos e{c^2}x$
And our $RHS = \cos e{c^2}x$ .
Hence, $LHS = RHS$ is proved.
Hence, we have proved that $1 + {\cot ^2}x = \cos e{c^2}x$ .

Note : We can also prove the identity $1 + {\cot ^2}x = \cos e{c^2}x$ with another method.
For this, we will be using the triangle.

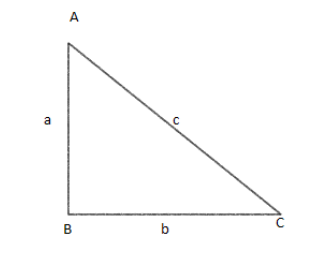
In the above triangle, using Pythagoras theorem,
$\to {a^2} + {b^2} = {c^2}$
Now, if we divide the above equation with ${a^2}$ , we get
$\to \dfrac{{{a^2}}}{{{a^2}}} + \dfrac{{{b^2}}}{{{a^2}}} = \dfrac{{{c^2}}}{{{a^2}}} \\\ \to 1 + {\left( {\dfrac{b}{a}} \right)^2} = {\left( {\dfrac{c}{a}} \right)^2} \\\$
Now, in $\Delta ABC$ , $\cot = \dfrac{b}{a}$ and $\cos ec = \dfrac{c}{a}$ . Hence, putting these values in above equation, we get
$\to 1 + {\cot ^2} = \cos e{c^2}$