Solveeit Logo
Login

Question

Question: How do you plot the polar coordinate \( \left( {3,{{150}^ \circ }} \right) \) ?...

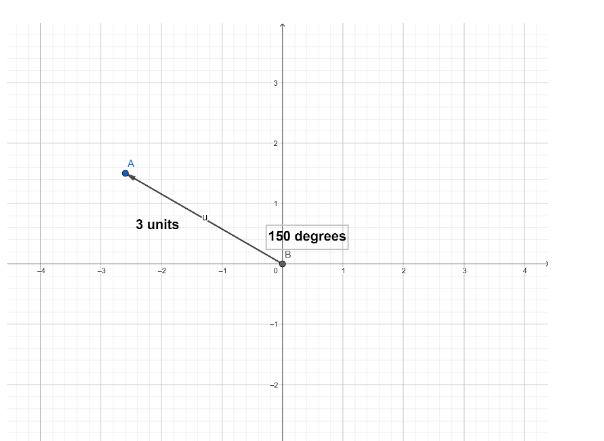
How do you plot the polar coordinate (3,150∘)\left( {3,{{150}^ \circ }} \right) ?

Explanation

Solution

Hint : As we know that the polar coordinate is like an alternative to the Cartesian coordinate system. On one hand the Cartesian system determines the position east and north of a fixed point while on the other hand the polar coordinates determine the location using direction and distance of a fixed point.

Complete step by step solution:
We first locate the angle of the polar coordinate plane and then we can plot the values.
As we know that a polar coordinate (r,θ)\left( {r,\theta } \right) in a Cartesian coordinate is (rcos⁡θ,rsin⁡θ)\left( {r\cos \theta ,r\sin \theta } \right) .
So the value of (3,150∘)\left( {3,{{150}^ \circ }} \right) in polar coordinate is (3cos⁡150∘,3sin⁡150∘)\left( {3\cos {{150}^ \circ },3\sin {{150}^ \circ }} \right) .
Now, we know that the value of cos⁡150∘\cos {150^ \circ } as (−32)\left( { - \dfrac{{\sqrt 3 }}{2}} \right) and sin⁡150∘\sin {150^ \circ } is (12)\left( {\dfrac{1}{2}} \right) .
So the Cartesian coordinate is (3×−32,3×12)\left( {3 \times \dfrac{{ - \sqrt 3 }}{2},3 \times \dfrac{1}{2}} \right) .
⇒(−332,32)\Rightarrow \left( {\dfrac{{ - 3\sqrt 3 }}{2},\dfrac{3}{2}} \right)
⇒(−332,32)\Rightarrow \left( {\dfrac{{ - 3\sqrt 3 }}{2},\dfrac{3}{2}} \right)
⇒(−2.59807,1.5)\Rightarrow \left( { - 2.59807,1.5} \right)
Hence we can plot these values as the polar coordinates.

Note : We should note that in the above solution we have used the angle sum identity to find the values of sin⁡150∘\sin {150^ \circ } and cos⁡150∘\cos {150^ \circ } . We can write sin⁡150∘\sin {150^ \circ } as sin⁡(180∘−30∘)\sin \left( {{{180}^ \circ } - {{30}^ \circ }} \right) .
Also we know that sin⁡(180∘−θ)=sin⁡θ\sin \left( {{{180}^ \circ } - \theta } \right) = \sin \theta . So, sin⁡(180∘−30∘)=sin⁡30∘\sin \left( {{{180}^ \circ } - {{30}^ \circ }} \right) = \sin {30^ \circ } which gives us the value sin⁡150∘=12\sin {150^ \circ } = \dfrac{1}{2} .
Similarly we can find the value of cos⁡150∘\cos {150^ \circ } as it can be written as cos⁡(180∘−30∘)=−cos⁡30∘\cos \left( {{{180}^ \circ } - {{30}^ \circ }} \right) = - \cos {30^ \circ } . There is a negative sign in the cosine value. So, cos⁡150∘=−32\cos {150^ \circ } = \dfrac{{ - \sqrt 3 }}{2} .