Question
Question: How do you plot the point \[\left( { - 5,60^\circ } \right)\] on a polar graph?...
How do you plot the point (−5,60∘) on a polar graph?
Solution
In order to graph a point on the polar plane, you should find theta first and then locate r on that line. This approach allows you to narrow the location of a point to somewhere on one of the lines representing the angle. From there, you can simply count out from the pole the radial distance.
Complete step by step solution:
Change the radius from negative to positive by adding or subtracting (as appropriate) 180∘ to or from the angle.
Here, let us add 180∘ to the angle (instead of subtracting):
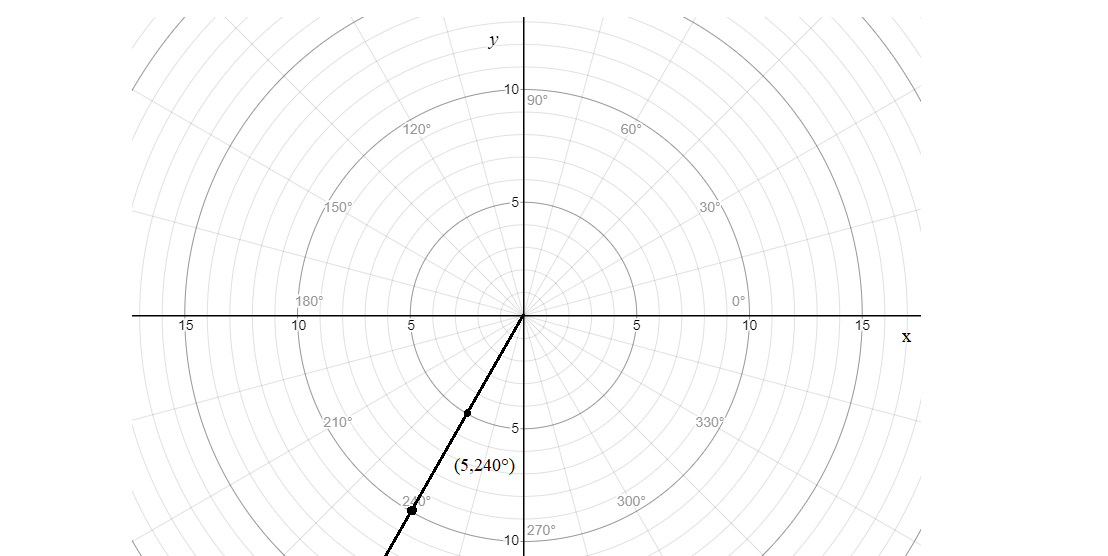
(−5,60∘)→(5,240∘)
Now, you merely find the intersection on the radius of 5 and the angle of 240∘ on the graph paper and draw a point as:
60∘=3π and 240∘=34π i.e., in graph we have: (−5,3π)→(5,34π).
Additional information:
Identify the type of polar equation, the polar equation is in the form, r=a−bcosθ. Since the equation passes the test for symmetry to the polar axis, we only need to evaluate the equation over the interval [0,π] and then reflect the graph about the polar axis.
Note: An angle whose measure is equal to 90 degrees is called a right angle, 180 degrees angle is called a straight angle and angles such as 270 degrees which are more than 180 but less than 360 degrees are called reflex angles. A 360 degrees angle is called a complete angle, hence by doing a complete rotation of two (or more) and adding or subtracting 360 degrees or a multiple of it before settling on the angle's terminal side, you can get an infinite number of angle measures, both positive and negative, for the same basic angle.
