Solveeit Logo
Login

Question

Question: How do you plot \( A\left( { - 6, - \dfrac{\pi }{6}} \right),B\left( { - 5, - \dfrac{\pi }{2}} \righ...

How do you plot A(−6,−π6),B(−5,−π2), and C(−8,−π4)A\left( { - 6, - \dfrac{\pi }{6}} \right),B\left( { - 5, - \dfrac{\pi }{2}} \right),\,and\,C\left( { - 8, - \dfrac{\pi }{4}} \right) in a polar coordinate system?

Explanation

Solution

Hint : In order to graph a polar coordinate ,draw a ray equal to the angular coordinate and mark the radius equal to radial coordinate, the point at which the ray drawn intersects the radius is our required polar coordinate on the cartesian plane.

Complete step-by-step answer :
There are two ways to determine a point on a plane, one is by the rectangular coordinates and another is by the Polar Coordinates.
Polar Coordinates (p,θ)(p,\theta ) is actually a 2D coordinate system in which every point on the plane is found by a distance pp from a reference point and an angle i.e. θ\theta from a reference direction.
where pp is the radial coordinate and θ\theta is known as the angular coordinate.
As per the question given we are given three polar coordinates as A(−6,−π6),B(−5,−π2), and C(−8,−π4)A\left( { - 6, - \dfrac{\pi }{6}} \right),B\left( { - 5, - \dfrac{\pi }{2}} \right),\,and\,C\left( { - 8, - \dfrac{\pi }{4}} \right) .
For Polar coordinate AA :
Radial coordinate = p1  =r1=−6{p_1}\,\, = {r_1} = - 6
Angular coordinate =θ1=−π6 = {\theta _1} = - \dfrac{\pi }{6}
First, we convert the Angular coordinate into degree
So, to convert into degree replace π\pi with 180
θ1=−16×180∘ θ1=−30∘   {\theta _1} = - \dfrac{1}{6} \times {180^ \circ } \\\ {\theta _1} = - {30^ \circ } \;
Now taking radius as p1  =r1=−6{p_1}\,\, = {r_1} = - 6 on the y-axis and angle measure as −30∘- {30^ \circ } , plot the point on the coordinate plane .
Similarly, identify the Radial coordinate and angular coordinate for the remaining points I.e. B and CB\,and\,C we have
For Polar coordinate AA :
Radial coordinate = p2  =r2=−5{p_2}\,\, = {r_2} = - 5
Angular coordinate =θ2=−π2 = {\theta _2} = - \dfrac{\pi }{2}
θ2=−12×180∘ θ2=−90∘   {\theta _2} = - \dfrac{1}{2} \times {180^ \circ } \\\ {\theta _2} = - {90^ \circ } \;
For Polar coordinate CC :
Radial coordinate = p2  =r2=−8{p_2}\,\, = {r_2} = - 8
Angular coordinate =θ3=−π4 = {\theta _3} = - \dfrac{\pi }{4}
θ3=−14×180∘ θ3=−45∘   {\theta _3} = - \dfrac{1}{4} \times {180^ \circ } \\\ {\theta _3} = - {45^ \circ } \;
Now plotting all the three points by taking the radial coordinate on the y-axis and measuring angle as per the radial coordinate. We obtain the graph of polar coordinate plane containing all the points as

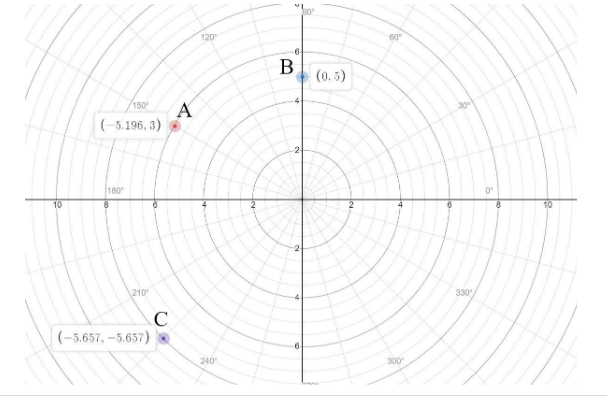
Therefore we have successfully plotted all the points on the polar coordinate plane .

Note : 1.One must be careful while determining the angular and radial coordinate.
2. To confirm you have correctly plotted our polar coordinate or not
Let Convert the polar coordinate into rectangular coordinates and if both are same then we can say that we have successfully plotted the polar coordinate correctly
Now to transformation by which we can find our rectangular coordinates (x,y)\left( {x,y} \right) is
x=rcos⁡θ y=rsin⁡θ   x = r\cos \theta \\\ y = r\sin \theta \;