Question

How do you plot $A\left( 4,{{0}^{\circ }} \right),B\left( 7,{{180}^{\circ }} \right)$ and $C\left( 9,{{45}^{\circ }} \right)$ in a polar coordinate system ?

Answer 1

Till now we have seen, rectangular coordinate system where both the points talked about the distance from the axes. One point talks about the distance from $x$- axis and the other point talks about the distance from the $y$- axis. But now we have a polar coordinate where one talks about the distance from the origin and the other tells us the direction in which this distance is to be measured. It is of the form $\left( r,\theta \right)$ where $r$ is the distance from the origin and $\theta$ is the measure of the angle. It can be degrees or radian.

Complete step by step answer:
So the polar coordinate is of the form $\left( r,\theta \right)$ where $r$ is the distance from the origin and $\theta$ is the measure of the angle. It can be degrees or radian. Let us graph these in degrees as of now.
Our angle,$\theta$ , is always measured from the polar axis which is the $x$- axis in the counterclockwise direction.
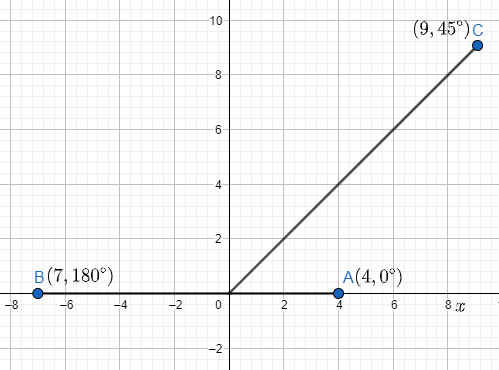
So now let us plot the points $A\left( 4,{{0}^{\circ }} \right),B\left( 7,{{180}^{\circ }} \right)$ and $C\left( 9,{{45}^{\circ }} \right)$.
The point $A\left( 4,{{0}^{\circ }} \right)$says that it is at a distance of $4$ units from the origin and at the angle ${{0}^{\circ }}$ from the axis. It means it is not making any angle with the axis. Hence it will be on the axis.
The point $B\left( 7,{{180}^{\circ }} \right)$ says that it is at a distance of $7$ units from the origin and at the angle ${{180}^{\circ }}=\pi$ from the x-axis. So this point can be written as $B\left( 7,\pi \right)$.
The point $C\left( 9,{{45}^{\circ }} \right)$ says that it is at a distance of $9$ units from the origin and at the angle ${{45}^{\circ }}=\dfrac{\pi }{4}$ from the x-axis. So this point can be written as $C\left( 9,\dfrac{\pi }{4} \right)$.
Upon plotting, we get this :

Note:
We should be very careful while plotting the points. It is important to know all the specifications of polar coordinates. Important points such as how to plot when the distance is negative or when the given angle is negative . For this, thorough practice is required so as to solve the question quickly and without any confusion. We should be alert while reading the question and notice whether the value of $\theta$ is given in degrees or radians.