Question

How do you plot $5i$ and find its absolute value?

Answer 1

In this question we have been given with a complex number which we will first represent in the general form of a complex number which is denoted as $a+bi$ where $a$ and $b$ are real numbers and $i$ is the imaginary part of the number which has the value $i=\sqrt{-1}$. The absolute value of the complex number can be found out using the formula $|z|=\sqrt{{{a}^{2}}+{{b}^{2}}}$where $z$ is the absolute value of the complex number.

Complete step by step answer:
We have the complex number given to us as $-5i$.
In this question we only have the imaginary part and no real part therefore, we will consider the value of the real part as $0$.
Therefore, the complex number can be represented in the general form $a+bi$ as $0-5i$, where the value of $a=0$ and $b=-5$.
Now to plot a complex number on the graph, the $x$ axis is considered to take the real part of the complex number and the $y$ axis takes the imaginary part of the number.
Therefore, the complex number in the form $a+bi$ is plotted as $(a,b)$.
Similarly, the complex number $0-5i$ will have coordinates as $(0,-5)$.
We can plot the point on the graph as:

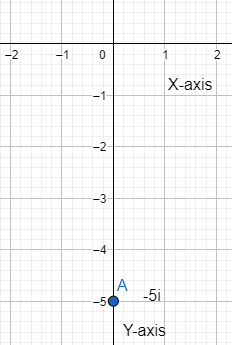
Where point $\text{A}$ denotes the complex number $0-5i$.
Now the absolute value of a complex number can be calculated using the formula $|z|=\sqrt{{{a}^{2}}+{{b}^{2}}}$
On substituting the values of $a$ and $b$ in the formula, we get:
$|z|=\sqrt{{{0}^{2}}+{{(-5)}^{2}}}$
On squaring the terms and adding, we get:
$|z|=\sqrt{25}$
On taking the square root, we get:
$|z|=\pm 5$
Since we have to take the absolute value, we get:
$|z|=5$, which is the absolute value of the complex number.

Note: It is to be remembered that a square of a negative term is positive. The exponential form and the polar form of a complex number should be remembered while doing these types of sums. The modulus of the complex number is also called as the absolute value which gives the actual distance between the origin and the complex number. In the above sum it can be seen that the number has an absolute value of $5$ therefore it is $5$ units further from the origin.