Solveeit Logo
Login

Question

Question: How do you locate the absolute extrema of the function \(f\left( x \right)={{x}^{3}}-12x\) on the cl...

How do you locate the absolute extrema of the function f(x)=x3−12xf\left( x \right)={{x}^{3}}-12x on the closed interval [0,4]\left[ 0,4 \right] ?

Explanation

Solution

Here in this question we have been asked to locate the absolute extrema of the given function f(x)=x3−12xf\left( x \right)={{x}^{3}}-12x in the closed interval [0,4]\left[ 0,4 \right]. We know that the absolute extrema of a function ff , that is continuous in a closed interval must occur at either a critical number for ff in the interval or at an endpoint of the interval.

Complete step by step answer:
Now considering from the question we have been asked to locate the absolute extrema of the given function f(x)=x3−12xf\left( x \right)={{x}^{3}}-12x in the closed interval [0,4]\left[ 0,4 \right].
From the basic concepts we know that the absolute extrema of a function ff , that is continuous in a closed interval must occur at either a critical number for ff in the interval or at an endpoint of the interval.
We know that the critical number for ff is the zero for f′f' .
Now we can say that f′(x)=3x2−12f'\left( x \right)=3{{x}^{2}}-12 since ddxxn=nxn−1\dfrac{d}{dx}{{x}^{n}}=n{{x}^{n-1}} .
The zeroes of f′f' will be generally given as
f′(x)=3(x2−4) ⇒f′(x)=3(x−2)(x+2) \begin{aligned} & f'\left( x \right)=3\left( {{x}^{2}}-4 \right) \\\ & \Rightarrow f'\left( x \right)=3\left( x-2 \right)\left( x+2 \right) \\\ \end{aligned} .
Therefore the zeroes of f′f' are 2,−22,-2 and in the closed interval [0,4]\left[ 0,4 \right] we have only one critical point for ff that is 22 and the endpoints will be 0,40,4.
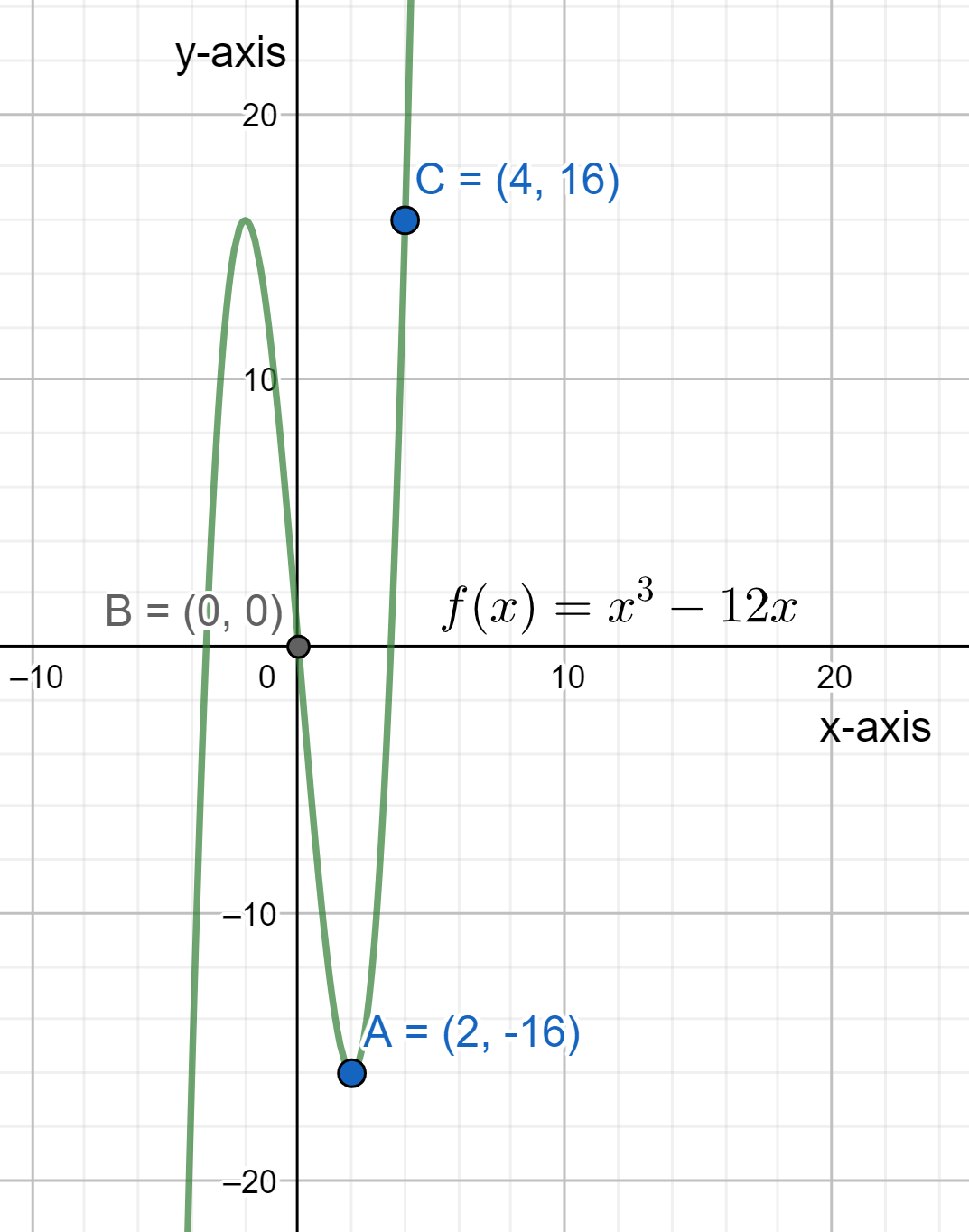
Hence we can say that the absolute extrema of the given function f(x)=x3−12xf\left( x \right)={{x}^{3}}-12x in the closed interval [0,4]\left[ 0,4 \right] will be located at x=0,2,4x=0,2,4 any of these points.
So now we need to evaluate the value of f(x)f\left( x \right) at these points.
At x=0x=0 , the value of f(x)=x3−12xf\left( x \right)={{x}^{3}}-12x will be zero.
At x=2x=2 , the value of f(x)=x3−12xf\left( x \right)={{x}^{3}}-12x will be −16-16 .
At x=4x=4 , the value of f(x)=x3−12xf\left( x \right)={{x}^{3}}-12x will be 1616 .

Therefore we can conclude that the absolute extrema of the given function f(x)=x3−12xf\left( x \right)={{x}^{3}}-12x in the closed interval [0,4]\left[ 0,4 \right]will be located at x=2x=2 (minimum) and x=4x=4 (maximum).

Note: While answering this type of questions we have to be sure with the calculations that we are going to perform and the concepts that we are going to apply in between the steps in order to answer them. Alternatively this question can be answered by using the graph of f(x)=x3−12xf\left( x \right)={{x}^{3}}-12x which is generally given as: