Question

How do you identify transformations in parent functions given $y = 2{\left( {x - 3} \right)^2}$?

Answer 1

In order to find the transformations in the parent function, we should first identify what kind of the parent function is there by checking out at the highest degree given in the equation. If the highest degree is one, then the parent function is a linear equation, if the degree is two then it’s a quadratic equation. After finding the parent function, we can see the changes made on the values, which are called transformations.

Complete step by step solution:
We are given with the function $y = 2{\left( {x - 3} \right)^2}$, while checking out the highest degree we get to know that it’s a quadratic equation, as its highest degree is two.
Since, we know that the basic function of a quadratic equation is $y = \pm a{\left( x \right)^2}$.
So according to that our parent function is $y = \pm a{\left( x \right)^2}$.
For transformations there are certain rules such as:

1. If for a function, $y = \pm a{\left( {x - h} \right)^2}$, $h > 0$, then the graph of the function shifts right of the parent function by $h$ units.
2. Similarly, if $h < 0$, then the graph of the function shifts left of the parent function by $h$ units.
   Since, we have our quadratic function $y = 2{\left( {x - 3} \right)^2}$, which represents a parabola and comparing it from the rule point (1.), we get that the parabola shifts right side of the parent function by $3$ units.
   Let’s see the graph of both the parent function that is $y = \pm a{\left( x \right)^2}$ and the transformed function that is $y = 2{\left( {x - 3} \right)^2}$, and we get:
   
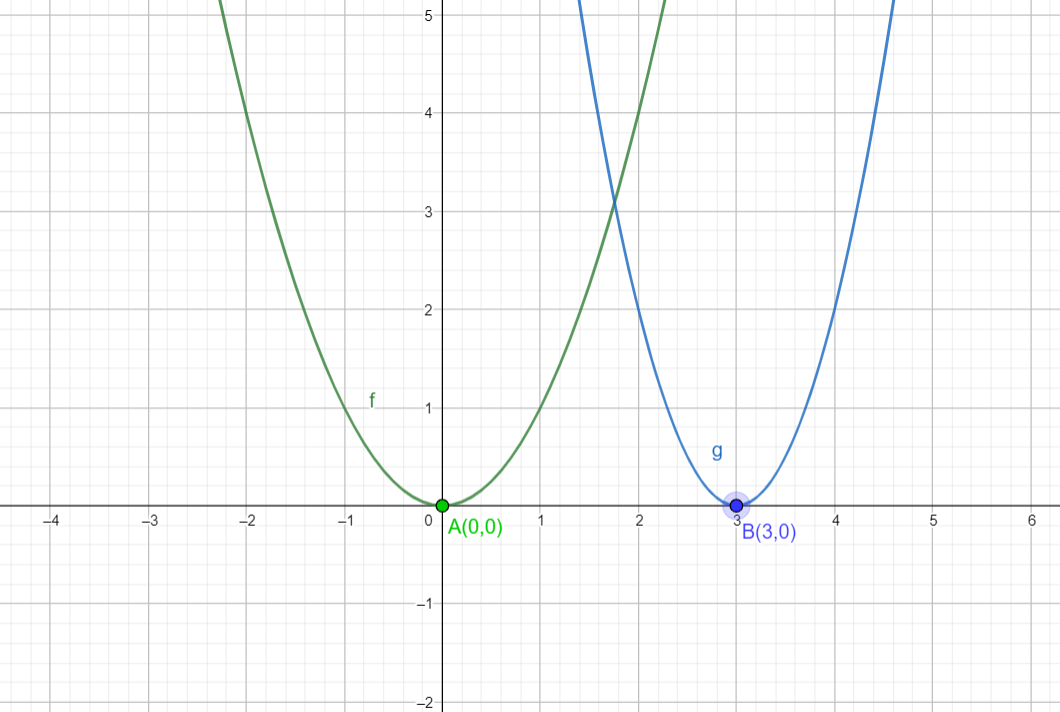
   The green parabola graph represents our parent function, and the blue parabolic graph represents our transformed function, which has shifted to $3$ units from the parent function.
   Therefore, there is a shift of $3$ units from the parent function in the given function $y = 2{\left( {x - 3} \right)^2}$.

Note:

1. There can also be an addition or subtraction in the parent functions, which would lead to a transformed function like: $g\left( x \right) = f\left( x \right) + 4$, the parent function is $f\left( x \right)$, when added some units gives a new transformed function $g\left( x \right)$.
2. Similarly, the same rules will work for linear and other functions.