Question

How do you identify the vertical and horizontal translations of sine and cosine from a graph and an equation?

Answer 1

For the function $y = f\left( x \right)$, the vertical translation is described by the equation $y = f\left( x \right) + a$ and horizontal translation is described by the equation $y = f\left( {x - a} \right)$. the vertical translation is described by the equation $y = f\left( x \right) + a$ such that if $a$ is greater than zero then the shift in the graph is upward from the original and if $a$ is less than zero then the shift in the graph is downward from the original. the horizontal translation is described by the equation $y = f\left( {x - a} \right)$ such that if $a$ is greater than zero then the shift in the graph is toward right from the original and if $a$ is less than zero then the shift in the graph is toward left from the original.

Complete step by step solution:
Consider the sine function as $y = \sin x$ and the cosine function as $y = \cos x$.

It is known that for a function $y = f\left( x \right)$, the vertical translation is described by the equation $y = f\left( x \right) + a$ such that if $a$ is greater than zero then the shift in the graph is upward from the original and if $a$ is less than zero then the shift in the graph is downward from the original.

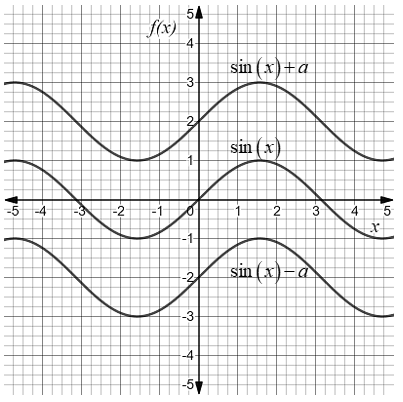
Therefore vertical translation of a sine function is written as $y = \sin x + a$ and the vertical translation of a cosine function is written as $y = \cos x + a$. Where $a$ cannot be zero.

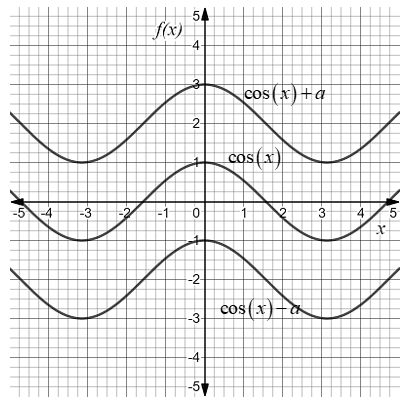
Thus, if we are able to write the sin function in the form $y = \sin x + a$ and the cosine function in the form $y = \cos x + a$ where in both cases $a \ne 0$ then it represents vertical translation in both trigonometric functions from the original.

In the graph, if sine functions or cosine functions wave is not symmetric to $x$-axis then there is a vertical shift in the graph from the original.

It is known that for a function $y = f\left( x \right)$, the horizontal translation is described by the equation $y = f\left( {x - a} \right)$ such that if $a$ is greater than zero then the shift in the graph is toward right from the original and if $a$ is less than zero then the shift in the graph is toward left from the original.

Therefore horizontal translation of a sine function is written as $y = \sin \left( {x - a} \right)$ and the horizontal translation of a cosine function is written as $y = \cos \left( {x - a} \right)$. Where $a$ cannot be zero.

Thus, if we are able to write the sin function in the form $y = \sin \left( {x - a} \right)$ and the cosine function in the form $y = \cos \left( {x - a} \right)$ where in both cases $a \ne 0$ then it represents horizontal translation in both trigonometric functions from the original.

In the graph, if sine functions or cosine functions wave is not symmetric to $y$-axis then there is a horizontal shift in the graph from the original.

Note: For horizontal shift, the function is $y = f\left( {x - a} \right)$ and for vertical shift, the function is $y = f\left( x \right) + a$ if the original function is $y = f\left( x \right)$. The horizontal translation of a sine function is written as $y = \sin \left( {x - a} \right)$ and the horizontal translation of a cosine function is written as $y = \cos \left( {x - a} \right)$. Where $a$ cannot be zero. The vertical translation of a sine function is written as $y = \sin x + a$ and the vertical translation of a cosine function is written as $y = \cos x + a$. Where $a$ cannot be zero.