Question

How do you identify critical points by looking at the graph?

Answer 1

To find the critical points in the graph, let us assume a function say $f\left( x \right)$. Now, just by looking at the graph of this function we can find the critical points by observing the points on the x axis at which the value of y is either maximum or minimum value with respect to the y values which are corresponding to the slightly greater or lesser than that x.

Complete step-by-step solution:
Let us assume a function says $f\left( x \right)$. In the above problem, we are asked to find the critical points by looking at the graph so the points where the derivative of the function $f\left( x \right)$ becomes 0 are the critical points of that function.
Let us take a function say$f\left( x \right)={{x}^{4}}-8{{x}^{2}}$ and in the below, we have drawn the graph of this function.

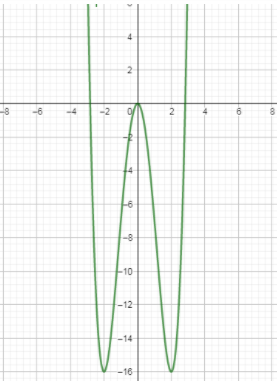
Now, to find the critical points of the above graph just by looking at it, we are going to see where the derivative of this function becomes zero. If a derivative of the function is 0 then you can find a minimum or a maximum point.
So, if you see the above graph, you will find the two minimums occurring at the points where x is +2 and -2. You can also see a point which is having a maximum with respect to its left and right side surroundings which is at $x=0$.
Hence, we have 3 critical points (i.e. 2, -2 and 0).

Note: If in the question, it is asked to find the critical points of the function then what you have to do is to take the derivative of this function and put that derivative to 0 and then find the values of x where this derivative becomes 0. Now, let us take the function which we have taken in the above solution.
$f\left( x \right)={{x}^{4}}-8{{x}^{2}}$
Now, we are going to find the derivative of the above function:
$\Rightarrow f'\left( x \right)=4{{x}^{3}}-16x$
Equating the above derivative to 0 we get,
$\Rightarrow f'\left( x \right)=4{{x}^{3}}-16x=0$
Taking x as common in the above equation we get,
$\Rightarrow x\left( 4{{x}^{2}}-16 \right)=0$
Also, we are going to take 4 as common from the L.H.S of the above equation we get,
$\Rightarrow 4x\left( {{x}^{2}}-4 \right)=0$
Equating $x\And \left( {{x}^{2}}-4 \right)$ to 0 we get,
$\begin{aligned} & x=0; \\\ & {{x}^{2}}-4=0 \\\ \end{aligned}$
We know the algebraic identity which states that:
$\Rightarrow {{a}^{2}}-{{b}^{2}}=\left( a-b \right)\left( a+b \right)$
Applying the above identity in the above equation we get,
$\begin{aligned} & \Rightarrow {{x}^{2}}-4=0 \\\ & \Rightarrow \left( x-2 \right)\left( x+2 \right)=0 \\\ \end{aligned}$
Equating each of the above two brackets to 0 we get,
$\begin{aligned} & x-2=0 \\\ & \Rightarrow x=2; \\\ & x+2=0 \\\ & \Rightarrow x=-2 \\\ \end{aligned}$
As you can see that we have got three critical points which are as same as which we got in the above solution.