Question

How do you graph $y = {x^2} - 6x + 2$?

Answer 1

In this problem, a quadratic equation is given. The equation of the curve is a parabola, and it has a vertex. In the general form, the equation is $y = a{x^2} + bx + c$. We will use the equation for the vertex of the parabola $a{\left( {x + d} \right)^2} + e$. Here, the formula for d is $d = \dfrac{b}{{2a}}$, and the formula of $e = c - \dfrac{{{b^2}}}{{4a}}$. Substitute the values of a, b, and c to find the vertex of the parabola.

Complete step by step solution:
In this question, the quadratic equation is given. The graph of the given expression is obtained.
Here, in the given parabola equation is:
$\Rightarrow y = {x^2} - 6x + 2$ ...(1)
Let us compare the above equation with the general form $y = a{x^2} + bx + c$.
So, the value of ‘a’ is 1, the value of ‘b’ is -6, and the value of ‘c’ is 2.
Now, let us consider the vertex form of a parabola.
$\Rightarrow a{\left( {x + d} \right)^2} + e$
Here, the formula of $d = \dfrac{b}{{2a}}$.
Put the value of a and b.
$\Rightarrow d = \dfrac{{ - 6}}{{2\left( 1 \right)}}$
$\Rightarrow d = \dfrac{{ - 6}}{2}$
That is equal to,
$\Rightarrow d = - 3$
The formula of $e = c - \dfrac{{{b^2}}}{{4a}}$.
Put the value of a, b and c.
$\Rightarrow e = 2 - \dfrac{{{{\left( { - 6} \right)}^2}}}{{4\left( 1 \right)}}$
$\Rightarrow e = 2 - \dfrac{{36}}{4}$
$\Rightarrow e = 2 - 9$
That is equal to,
$\Rightarrow e = - 7$
Now, put these values in the below equation.
$\Rightarrow a{\left( {x + d} \right)^2} + e$
Therefore,
$\Rightarrow 1{\left( {x - 3} \right)^2} - 7$
That is equal to,
$\Rightarrow {\left( {x - 3} \right)^2} - 7$
Use the vertex form, $y = a{\left( {x - h} \right)^2} + k$, to determine the values of a, h, and k.
The value a is 1, the value of h is 3, and the value of k is -7.
Since the value of a is positive, the parabola opens up.
Let us find the vertex $\left( {h,k} \right)$.
Therefore, the vertex is (3, -7).
Now, let us find the distance from the vertex to a focus of the parabola by using the formula:
$\Rightarrow P = \dfrac{1}{{4a}}$
Put the value of a is 1.
$\Rightarrow P = \dfrac{1}{{4\left( 1 \right)}}$
That is equal to,
$\Rightarrow P = \dfrac{1}{4}$
Now, let us find the focus. The focus of a parabola can be found by adding P to the y-coordinate k is the parabola opens up or down.
The formula for focus is:
$\Rightarrow \left( {h,k + p} \right)$
Put the value of h, k, and p.
$\Rightarrow \left( {3, - 7 + \dfrac{1}{4}} \right)$
Let us take LCM.
$\Rightarrow \left( {3,\dfrac{{ - 28 + 1}}{4}} \right)$
That is equal to,
$\Rightarrow \left( {3,\dfrac{{ - 27}}{4}} \right)$
Now, find the axis of symmetry by finding the line that passes through the vertex and the focus.
That is equal to,
$\Rightarrow x = 3$
Now, the directrix of a parabola is the horizontal line found by subtracting p from the y-coordinate k of the vertex if the parabola opens up or down.
$\Rightarrow y = k - p$
Put the value of k and p.
$\Rightarrow y = - 7 - \dfrac{1}{4}$
Take LCM.
$\Rightarrow y = \dfrac{{ - 28 - 1}}{4}$
That is equal to,
$\Rightarrow y = \dfrac{{ - 29}}{4}$
The graph of the given equation is as below.

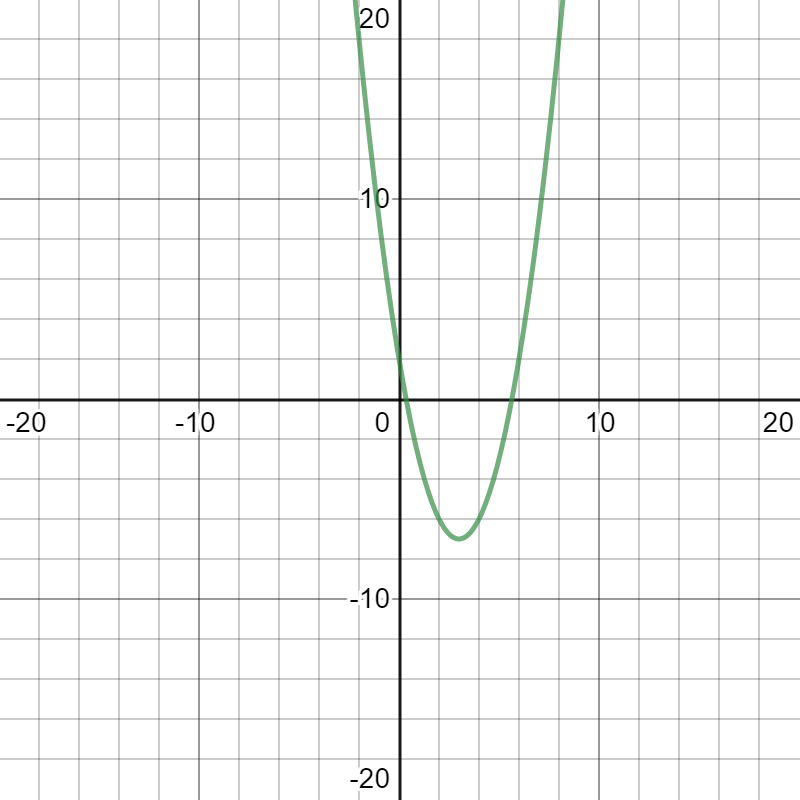
Note: We should remember the formulas for the vertex is $\left( {h,k} \right)$, the distance from the vertex to a focus of the parabola is $P = \dfrac{1}{{4a}}$, the focus of a parabola focus is $\left( {h,k + p} \right)$, the directrix of a parabola is $y = k - p$.