Solveeit Logo
Login

Question

Question: How do you graph \(y = {x^2} - 6x + 11\)?...

How do you graph y=x2−6x+11y = {x^2} - 6x + 11?

Explanation

Solution

Since the leading coefficient is positive, this quadratic equation will be upward parabola. Find the nature of its roots. If the roots are imaginary then its graph will never touch or cut the x−x - axis. Finally find the position of its vertex to identify whether it lies on the positive side or negative side of the x−x - axis.

Complete step-by-step solution:
According to the question, a quadratic equation is given to us and we have to show the process to draw its graph.
The given quadratic equation is:
⇒y=x2−6x+11\Rightarrow y = {x^2} - 6x + 11
Since its leading coefficient is positive, we know that its graph will be an upward parabola.
Nature of roots of a quadratic equation can be determined by its discriminant. For a quadratic equation y=ax2+bx+cy = a{x^2} + bx + c, the discriminant is D=b2−4acD = {b^2} - 4ac.
So calculating the determinant of the given quadratic equation, we have:
⇒D=(−6)2−4×1×11 ⇒D=−8 \Rightarrow D = {\left( { - 6} \right)^2} - 4 \times 1 \times 11 \\\ \Rightarrow D = - 8
Determinant is negative means the equation has all imaginary roots. So the graph of this function will never cut or touch x−x - axis.
Till now we have the information that the graph will be an upward parabola not touching or cutting x−x - axis i.e. lying above x−x - axis.
We still have to find the position of its vertex to identify whether it will lie on the positive side or negative side of the x−x - axis.
The x−x - coordinate of the vertex is calculated by differentiating its equation and putting it to zero. Doing so, we’ll get:
⇒y=x2−6x+11 ⇒dydx=2x−6 \Rightarrow y = {x^2} - 6x + 11 \\\ \Rightarrow \dfrac{{dy}}{{dx}} = 2x - 6
Putting derivative to zero, we’ll get:
⇒2x−6=0 ⇒x=3 \Rightarrow 2x - 6 = 0 \\\ \Rightarrow x = 3
Thus the vertex of the parabola will be at x=3x = 3.
Further, if we put x=0x = 0 in the equation of the parabola, we have:
⇒y(0)=02−6(0)+11 ⇒y(0)=11 \Rightarrow y\left( 0 \right) = {0^2} - 6\left( 0 \right) + 11 \\\ \Rightarrow y\left( 0 \right) = 11
So the parabola will cut the y−y - axis at (0,11)\left( {0,11} \right).
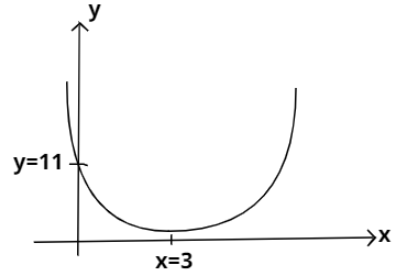
To conclude our observations of the graph of y=x2−6x+11y = {x^2} - 6x + 11, we have:
(1) The graph will be an upward parabola lying above the x−x - axis.
(2) Its vertex will be at a point where x=3x = 3.
(3) It will cut y−y - axis at (0,11)\left( {0,11} \right).
Based on these points, the graph can be drawn as shown below:

Note: (1) If the leading coefficient of the parabola is negative the graph of the parabola will be opening downwards.
(2) If the discriminant of the quadratic equation is not negative then the roots of the equation will be real and the parabola will certainly cut or touch the x−x - axis.
(3) If the discriminant is positive then the parabola will cut the x−x - axis and if the discriminant is zero then it will only touch the x−x - axis.