Question

How do you graph $y = {x^2} - 5$ ?

Answer 1

The given equation is a parabola. To graph this parabola firstly we need to find the vertex, the line of symmetry, focus, and the directrix. Plot these coordinates on the graph to get a rough sketch of an upward parabola with $y$-axis as the line of symmetry.

Formula used: The general equation of an upward-facing parabola is,${(x - h)^2} = 4a(y - k)$
The focus is given by the coordinates, $(h,k + a)$
The directrix is given by the equation, $y = k - a$

Complete step-by-step answer:
The given equation is, $y = {x^2} - 5$
The given equation is in the form of the Parabola formula,$y = a{x^2} + bx + c$
The general equation of a parabola whose vertex is at $\left( {h,k} \right)$ is,
$\Rightarrow$ ${(x - h)^2} = 4a{(y - k)^{}}$
Here, $4\;a$ is the length of the latus rectum.
We can rearrange our equation as,
$\Rightarrow ({x^2}) = (y + 5)$
$\Rightarrow {(x - 0)^2} = 4 \times \dfrac{1}{4}(y + 5)$
On comparing this with the general equation of parabola we get,
$\Rightarrow (h,k) = (0, - 5)$
which is the vertex of the parabola.
The length of the latus rectum is $4\;a$ which is $1$ in our equation.
The LHS of our equation $(x - 0)$is the line of symmetry.
$\Rightarrow x = 0$ is $y$-axis.
Focus is given by the expression $(h,k + a)$
$\Rightarrow (0, - 5 + \dfrac{1}{4})$
$\Rightarrow \left( {0,\dfrac{{ - 19}}{4}} \right)$is the focus of the given parabola.
Directrix is given by $y = k - a$
$\Rightarrow y = - 5 - \dfrac{1}{4}$
$\Rightarrow y = \dfrac{{ - 21}}{4}$
is the directrix of the given parabola equation.
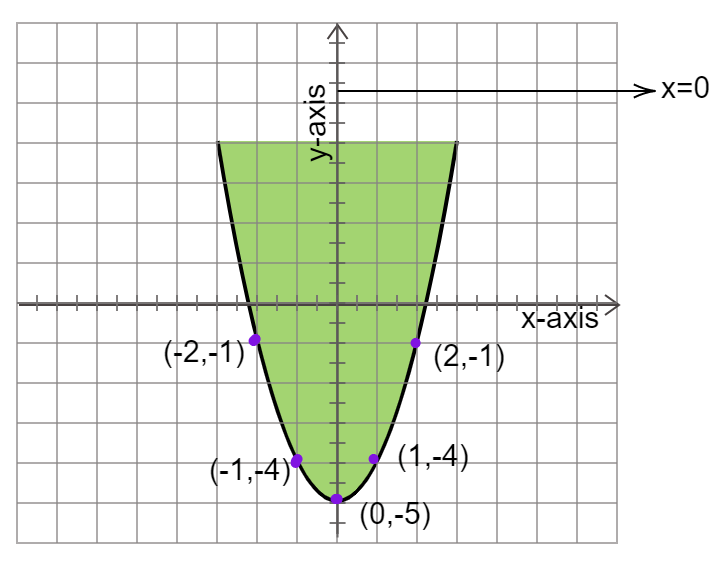
Let us roughly take some more points to get an exact sketch of the parabola.
When $x = 1$,$y = {1^2} - 5 \Rightarrow y = - 4$
$\Rightarrow$ $(1, - 4)$ satisfies the equation.
When $x = - 1$,$y = {( - 1)^2} - 5 \Rightarrow y = - 4$
$\Rightarrow$ $( - 1, - 4)$ satisfies the equation.
When $x = 2$,$y = {2^2} - 5 \Rightarrow y = - 1$
$\Rightarrow$ $(2, - 1)$ satisfies the equation.
When $x = - 2$,$y = {( - 2)^2} - 5 \Rightarrow y = - 1$
$\Rightarrow$ $( - 2, - 1)$ satisfies the equation.
Now, on plotting all these points on the graph we get,

The diagram showing the Focus, Directrix, and the line of symmetry of the parabola is given below.

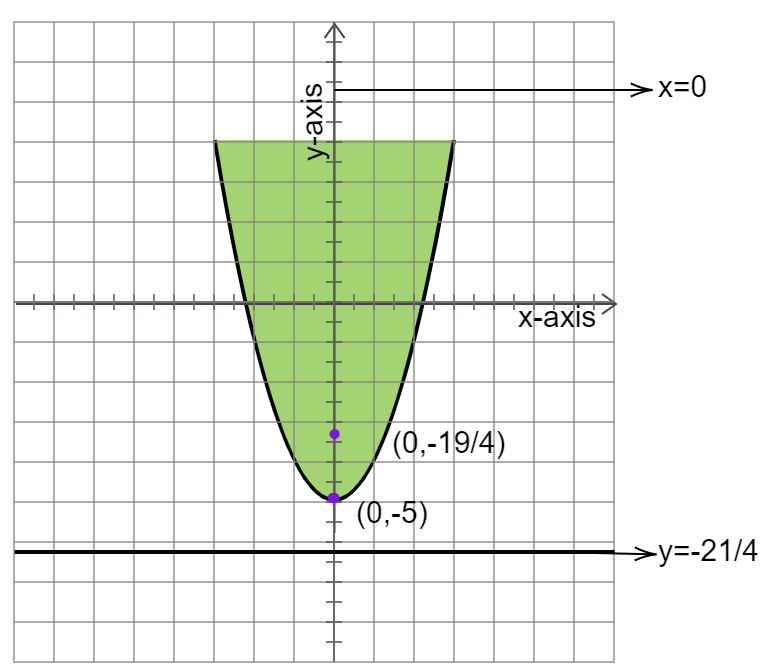
$\Rightarrow$ $y = \dfrac{{ - 21}}{4}$ is the Directrix of the given parabola and $(0,\dfrac{{ - 19}}{4})$ is the focus of the parabola.
$\Rightarrow$ $x = 0$ is the Line of symmetry of the parabola.

Note:
The vertex always lies in the midway between the Focus and the directrix of the Parabola. The focal diameter of the parabola is known as the Latus rectum of the parabola which is the length of the line passing through the focus crossing the parabola.