Solveeit Logo
Login

Question

Question: How do you graph \(y={{x}^{2}}-2x-5\)?...

How do you graph y=x2−2x−5y={{x}^{2}}-2x-5?

Explanation

Solution

We equate the given equation of parabolic curve with the general equation of (x−α)2=4a(y−β){{\left( x-\alpha \right)}^{2}}=4a\left( y-\beta \right). We find the number of x intercepts and the value of the y intercept. We also find the coordinates of the focus to place the curve in the graph.

Complete step-by-step solution:
The given equation y=x2−2x−5y={{x}^{2}}-2x-5 is a parabolic curve.
We convert the equation into a square form and get
y=x2−2x−5=x2−2x+1−6 ⇒(x−1)2=(y+6) \begin{aligned} & y={{x}^{2}}-2x-5={{x}^{2}}-2x+1-6 \\\ & \Rightarrow {{\left( x-1 \right)}^{2}}=\left( y+6 \right) \\\ \end{aligned}
We equate (x−1)2=(y+6){{\left( x-1 \right)}^{2}}=\left( y+6 \right) with the general equation of parabola (x−α)2=4a(y−β){{\left( x-\alpha \right)}^{2}}=4a\left( y-\beta \right).
For the general equation (α,β)\left( \alpha ,\beta \right) is the vertex. 4a is the length of the latus rectum. The coordinate of the focus is (α,β+a)\left( \alpha ,\beta +a \right).
This gives the vertex as (1,−6)\left( 1,-6 \right). The length of the latus rectum is 4a=14a=1 which gives a=14a=\dfrac{1}{4}.

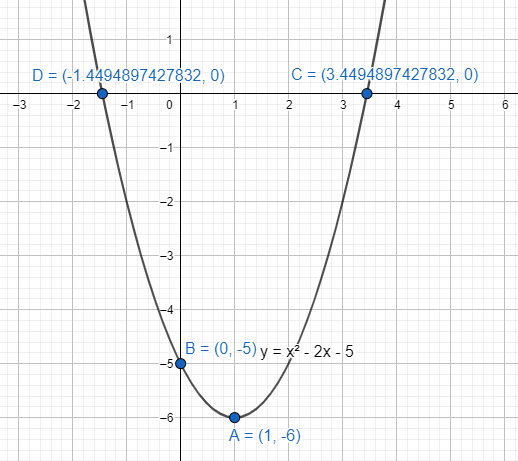
We have to find the possible number of x intercepts and the value of the y intercept. The curve cuts the X and Y axis at certain points and those are the intercepts.
We first find the Y-axis intercepts. In that case for the Y-axis, we have to take the coordinate values of x as 0. Putting the value of x=0x=0 in the equation y=x2−2x−5y={{x}^{2}}-2x-5, we get
y=02−2×0−5=−5y={{0}^{2}}-2\times 0-5=-5
So, the intercept point for Y-axis is (0,−5)\left( 0,-5 \right). There is only one intercept on both Y-axis.
We first find the X-axis intercepts. In that case for X-axis, we have to take the coordinate values of y as 0. Putting the value of y=0y=0 in the equation y=x2−2x−5y={{x}^{2}}-2x-5, we get

& y={{x}^{2}}-2x-5 \\\ & \Rightarrow 0={{x}^{2}}-2x-5 \\\ & \Rightarrow {{\left( x-1 \right)}^{2}}=6 \\\ & \Rightarrow x=1\pm \sqrt{6} \\\ \end{aligned}$$ **The intercept point for X-axis is $\left( 1\pm \sqrt{6},0 \right)$. There are two intercepts for the Y-axis.** **Note:** The minimum point of the function $y={{x}^{2}}-2x-5$ is $\left( 1,-6 \right)$. The graph is bounded at that point. But on the other side the curve is open and not bounded. The general case of parabolic curve is to be bounded at one side to mark the vertex.