Question

How do you graph y = tan3x?

Answer 1

If we need to find the values at different angles, we apply trigonometric ratios. Tangent function is formed by dividing sine and cosine function. Also, we should know about the even and odd functions. In this question, we should know about basic function tanx and we have drawn a graph of tan3x.

Complete step by step answer:
Some basic trigonometric functions are:
$\Rightarrow$ Sine (sin)
$\Rightarrow$Cosine (cos)
$\Rightarrow$Tangent (tan)
So, when we say $\tan \theta$, here $\theta$ means angle in degrees.
Derived functions are derived from the basic trigonometric functions. They are as follows:
$\Rightarrow$cosec$\theta$ = $\dfrac{1}{\sin \theta }$
$\Rightarrow$sec$\theta$ = $\dfrac{1}{\cos \theta }$
$\Rightarrow$tan$\theta$ = $\dfrac{\sin \theta }{\cos \theta }$ = $\dfrac{1}{\cot \theta }$
$\Rightarrow$cot$\theta$ = $\dfrac{1}{\tan \theta }$ = $\dfrac{\cos \theta }{\sin \theta }$
You know what exactly tan$\theta$ is? Let’s find it out.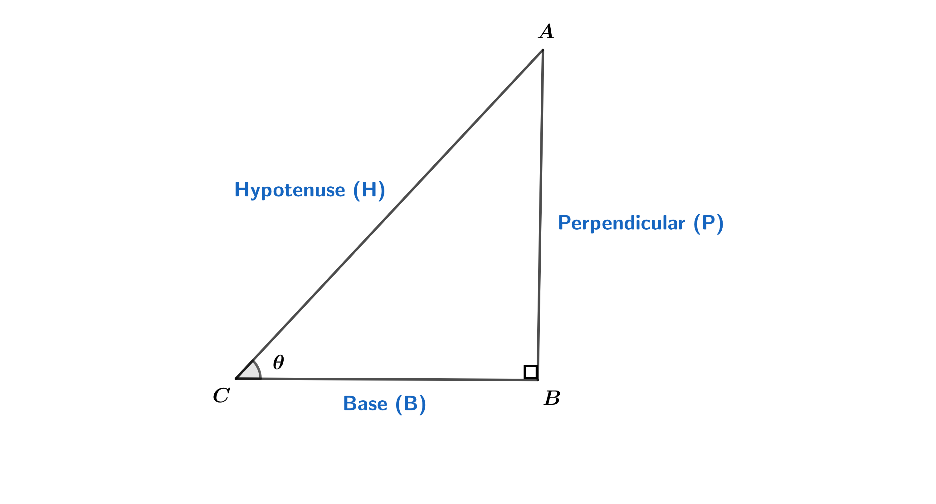

So, from above figure,
$\Rightarrow$ sin$\theta$ = $\dfrac{perpendicular(P)}{hypotenuse(H)}$
$\Rightarrow$cos$\theta$ = $\dfrac{base(B)}{hypotenuse(H)}$
$\begin{aligned} & \Rightarrow \tan \theta =\dfrac{\sin \theta }{\cos \theta } \\\ & \Rightarrow \tan \theta =\dfrac{perpendicular(P)}{base(B)} \\\ \end{aligned}$
Now, let’s see some even and odd functions.
$\Rightarrow$sin(-x) = -sinx
$\Rightarrow$ cos(-x) = cosx
$\Rightarrow$ tan(-x) = -tanx
$\Rightarrow$ cot(-x) = -cotx
$\Rightarrow$ cosec(-x) = -cosecx
$\Rightarrow$sec(-x) = secx
Now, let’s make a table of trigonometric ratios for basic trigonometric functions i.e. sin, cos, tan, cot, sec and cosec.

Trigonometric ratios(angle $\theta$ in degrees)	${{0}^{\circ }}$	${{30}^{\circ }}$	${{45}^{\circ }}$	${{60}^{\circ }}$	${{90}^{\circ }}$
sin$\theta$	0	$\dfrac{1}{2}$	$\dfrac{1}{\sqrt{2}}$	$\dfrac{\sqrt{3}}{2}$	1
cos$\theta$	1	$\dfrac{\sqrt{3}}{2}$	$\dfrac{1}{\sqrt{2}}$	$\dfrac{1}{2}$	0
tan$\theta$	0	$\dfrac{1}{\sqrt{3}}$	1	$\sqrt{3}$	$\infty$
cosec$\theta$	$\infty$	2	$\sqrt{2}$	$\dfrac{2}{\sqrt{3}}$	1
sec$\theta$	1	$\dfrac{2}{\sqrt{3}}$	$\sqrt{2}$	2	$\infty$
cot$\theta$	$\infty$	$\sqrt{3}$	1	$\dfrac{1}{\sqrt{3}}$	0

Graph of tan3x is quite similar to tanx.
As period of y = tan3x so, tan3x takes all the values with interval length of $\dfrac{\pi }{3}$.
First, let’s see the graph of tanx.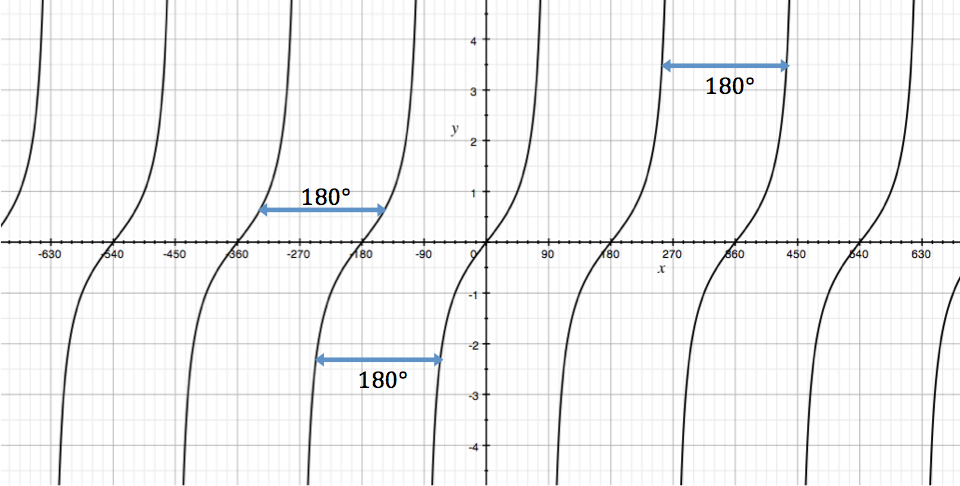

Now, let’s see the graph of tan3x.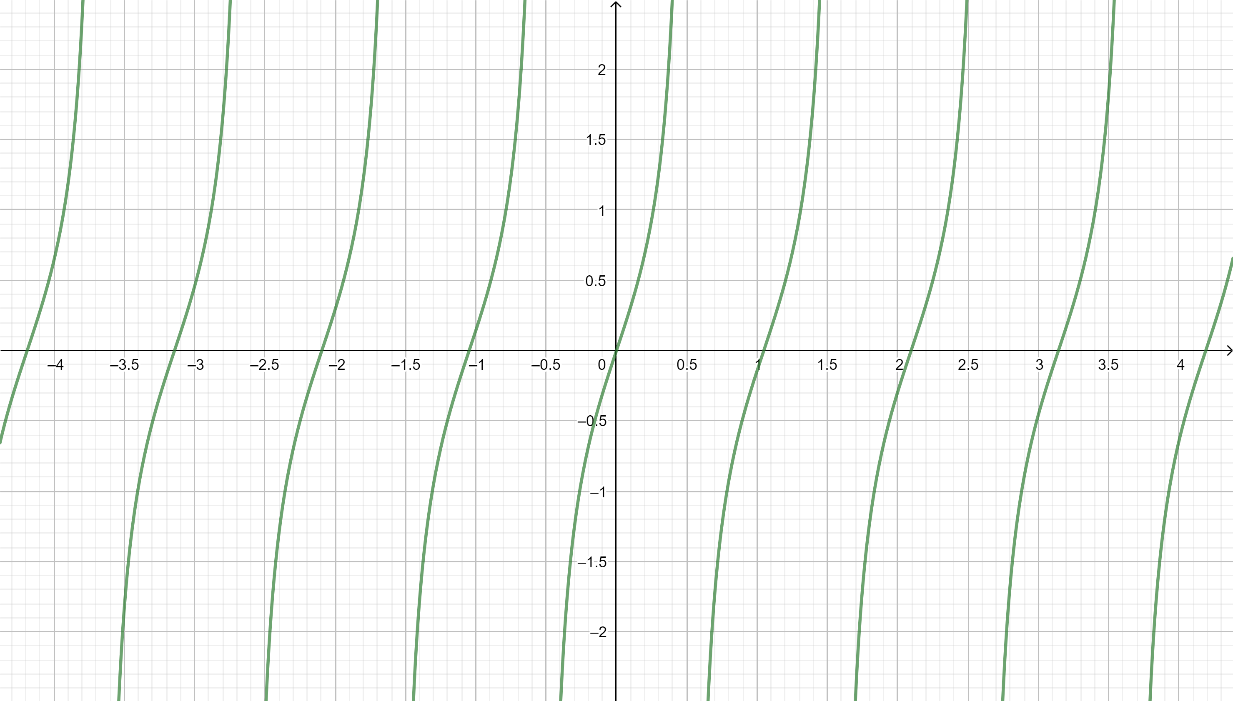

Note: Students should remember all the functions and trigonometric ratios before solving any question related to trigonometry. In this question, the main purpose of the question is to sketch the graph of tan3x which should be done neatly.