Question

How do you graph $y=\tan \left( \dfrac{x}{3} \right)$ and include two full periods?

Answer 1

Hint : In the given question, we have been asked to graph $y=\tan \left( \dfrac{x}{3} \right)$ and include two full periods. In order to solve the question, we will take the general equation and find the period. The general equation of $y=\tan \left( \dfrac{x}{3} \right)$ will be $y=a\tan \left( b\left( x+c \right) \right)+d$ and the period is given by $\dfrac{\pi }{\left| b \right|}$ .
We will equate the given equation with the general equation and find the solution.

Complete step-by-step answer :
We have given that,
$y=\tan \left( \dfrac{x}{3} \right)$
Finding the asymptote:
Vertical asymptote;
For any $y=\tan x$ , vertical asymptote occurs at $x=\dfrac{\pi }{2}+n\pi$ , where ‘n’ is an integer. Using the basic period for $y=\tan x,\left( -\dfrac{\pi }{2},\dfrac{\pi }{2} \right)$ .
The general equation of $y=\tan \left( \dfrac{x}{3} \right)$ will be $y=a\tan \left( b\left( x+c \right) \right)+d$
Therefore,
The vertical asymptote for $y=\tan \left( \dfrac{x}{3} \right)$ .
$\left( \dfrac{x}{3} \right)=-\dfrac{\pi }{2}\ \ or\ \ \left( \dfrac{x}{3} \right)=\dfrac{\pi }{2}$
Solving for the value of ‘x’, we will get
$x=-\dfrac{3\pi }{2},\dfrac{3\pi }{2}$
Therefore,
The basic period for $y=\tan \left( \dfrac{x}{3} \right)$ will occur at $\left( -\dfrac{3\pi }{2},\dfrac{3\pi }{2} \right)$ .
No horizontal and oblique asymptote occurs as tangent function can only have vertical asymptote.
Finding the period: $\dfrac{\pi }{\left| b \right|}$
As we know that,
$\dfrac{1}{3}$ is approximately equal to $0.\overline{3}$ which is positive so eliminating the absolute value.
Therefore,
Period = $\dfrac{\pi }{\dfrac{1}{3}}$ = $3\pi$
And it is given in the question that $y=\tan \left( \dfrac{x}{3} \right)$ and include two full periods.
Thus,
$2\times 3\pi =6\pi$
Now,
Amplitude of $y=\tan \left( \dfrac{x}{3} \right)$ :
Since the graph of the tangent function is not maximum and the minimum value, thus no amplitude.
Shift of $y=\tan \left( \dfrac{x}{3} \right)$ :
The shift has two parts. One being the phase shift of the graph and one being vertical shift.
There will be no phase shift and the vertical shift.
Hence, the graph of the $y=\tan \left( \dfrac{x}{3} \right)$ is as follows;

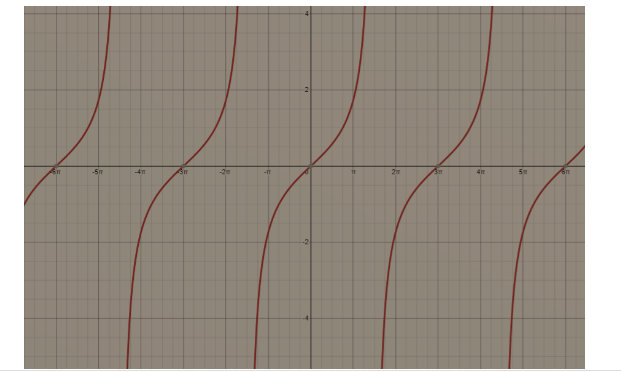
Note : Amplitude is the vertical distance from the x-axis to the highest or the lowest point on a sine or cosine curve. Period of each generalized trigonometric function curve is the length of the one complete cycle. Phase shift is the amount that the curve is shifted to the left or the right. Amplitude and period are always the positive number whereas phase shift can be of both the signs.