Question

How do you graph $y=\tan \left( 2x \right)$?

Answer 1

For solving this question, we should know that if $f\left( x \right)$ (that is called a function of x) has a period of T, then the period of $f\left( kx \right)$ will be $\dfrac{T}{k}$. In solving this question, first we will calculate the period of $\tan \left( 2x \right)$. After that we will draw the graph of $\tan \left( 2x \right)$.

Complete step by step answer:
Let us solve the question.
As we know that period of $\tan \left( x \right)$ is $\pi$.
The graph of $y=\tan \left( x \right)$ is:

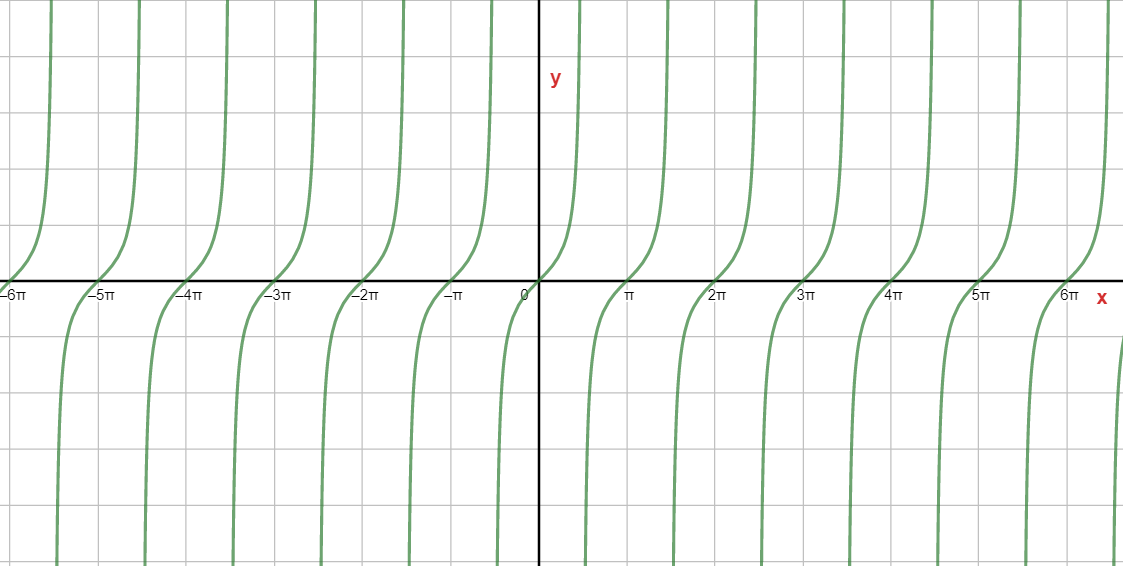
Here, in the above graph, the value of x is given along x-axis and the value of $\tan x$ is given along y-axis.
As it is seen from the above graph that after every $\pi$ units, the $\tan x$ is repeating.
Let us find out the period of $\tan 2x$.
As we know that if period of a function $f\left( x \right)$ is T. Then, the period of $f(kx)$ is $\dfrac{T}{k}$ , where k is any real number.
Now, applying the above procedure in $\tan x$.
If $\tan x$ has a period of $\pi$
Then, we can say that
$\tan \left( 2x \right)$ has a period of $\dfrac{\pi }{2}$.
If $\tan x$ has a period of $\pi$, that means the graph of $\tan x$ is repeating after every $\pi$ units.
Then, $\tan \left( 2x \right)$ has a period of $\dfrac{\pi }{2}$, that means the graph of $\tan \left( 2x \right)$ will be repeating after every $\dfrac{\pi }{2}$ units.
Therefore, the graph of $\tan \left( 2x \right)$ will be:

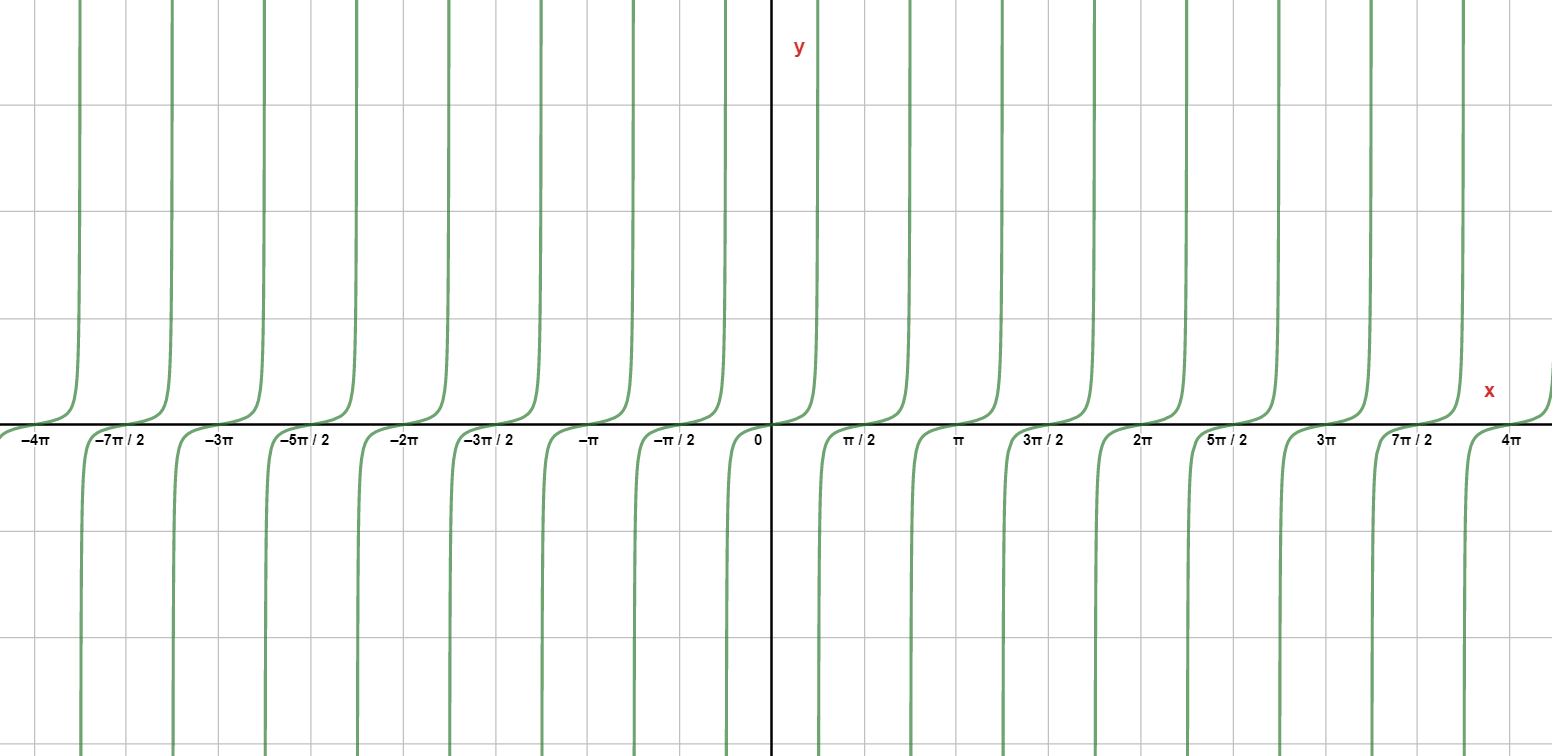
In the above graph, the value of x is given along the x-axis and the value of $\tan \left( 2x \right)$ is given along the y-axis.
We can see from the above graph that the $\tan \left( 2x \right)$ is repeating after every $\dfrac{\pi }{2}$ units.
This graph is 2 times faster than first.

Note: Remember the period of trigonometric functions to solve this type of problems. And we should have a proper knowledge in periodic functions also. As stated above that the period of $f(kx)$ is $\dfrac{T}{k}$. Here, k can be any real number. But, make sure that k should not be zero. Otherwise, the process will be wrong in that case.