Question

How do you graph $y=\tan 2x$?

Answer 1

To graph the above trigonometric function, we will first graph the trigonometric function $y=\tan x$ then the function which we have to graph has the angle two times of that of $\tan x$ so the values of x that this $\tan 2x$ will be half of that of $\tan x$ to achieve the same pattern of the graph as that of $\tan x$.

Complete step by step answer:
The trigonometric function which we have to draw on the graph is as follows:
$y=\tan 2x$
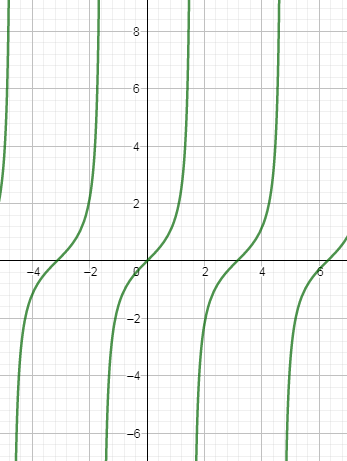
To draw the above graph, we are going to draw $y=\tan x$ first and this graph of $y=\tan x$ we already know from the standard graphs of the trigonometric functions. So, the graph of $y=\tan x$ is as follows:

Now, in the graph of $y=\tan 2x$, the values of x will be changed with respect to $\tan x$. And we have demonstrated the change as follows: We know that $\tan x=1$ is possible when $x=\dfrac{\pi }{4}$ and $\tan 2x=1$ when $2x=\dfrac{\pi }{4}$ and then the value of x is calculated by dividing 2 on both the sides of the equation in x.
$\begin{aligned} & \dfrac{2x}{2}=\dfrac{\pi }{2\left( 4 \right)} \\\ & \Rightarrow x=\dfrac{\pi }{8} \\\ \end{aligned}$
As you can see that the value of x in $\tan 2x$ becomes one half of the value of x in $\tan x$.
The values of x at which $\tan 2x$ is drawn is half of the values of x at which $\tan x$ is drawn so keeping in mind this concept we are going to draw the graph of $\tan 2x$.

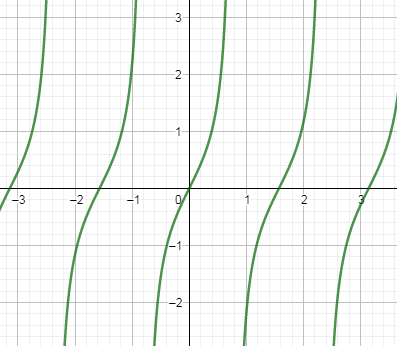
Hence, we have drawn the graph of $y=\tan 2x$ as follows:

Note: In the above graph of $y=\tan 2x$ , as you can see that the function becomes 0 when the value of x is around 1.5 and we know that the value of $\dfrac{\pi }{2}=1.57$ so $\tan 2x=0$ when $x=\dfrac{\pi }{2}$.
In the graph of $\tan x$, it will be 0 in the multiple of $\pi$ means when $x=\pi$ then the function becomes 0 and in the graph of $\tan 2x$, it is 0 when $x=\dfrac{\pi }{2}$ and as this value of x is half of $\pi$. Hence, we have drawn the correct graph.