Question

How do you graph $y = \sin x + x$

Answer 1

First, find the derivative of the trigonometric function. Then determine the possible values of $x$ at which the function is equal to zero. We will find the value of the function when $x$ reaches to infinity.

Complete step-by-step answer:
We know that the graph of a function is defined for all $x$ which belong to real number. First, determine the value of the derivative of the function.
$\Rightarrow y' = {\left( {\sin x} \right)^\prime } + x'$
Find the derivative of the expression.
$\Rightarrow y' = \cos x + 1$
The range of $\cos x = \left[ { - 1,1} \right]$. Equate the differentiation of the function to zero to compute the value of $x$.
$\Rightarrow y' = 0$
$\Rightarrow \cos x + 1 = 0$
$\Rightarrow \cos x = - 1$
Now we will apply the general solution of $\cos x = \cos \alpha$
Therefore, the value of $\cos x = - 1$when $x = n\pi$
Now, apply the limits to the function.
$\Rightarrow \mathop {\lim }\limits_{x \to - \infty } y = - \infty$
And
$\Rightarrow \mathop {\lim }\limits_{x \to \infty } y = \infty$
Now find the second derivative of the function by again differentiating the equation.
$\Rightarrow y'' = {\left( {\cos x} \right)^\prime } + {\left( 1 \right)^\prime }$
$\Rightarrow y'' = - \sin x$
Now, equate the second derivative of the function to zero to compute the value of $x$.
$\Rightarrow - \sin x = 0$
Now we will apply the general solution of $\sin x = 0$
Therefore, the value of $\sin x = 0$ when $x = n\pi$
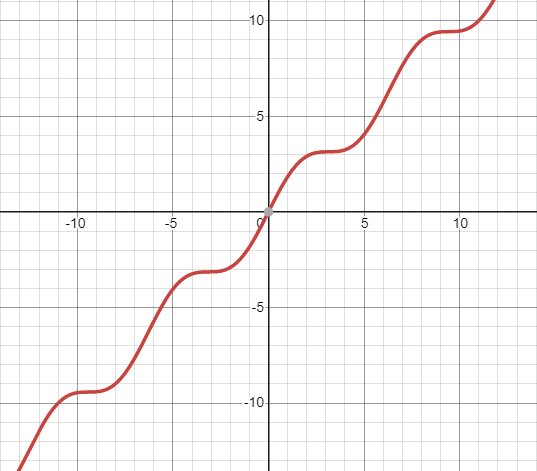
Here, the inflection points for $x$ is equal to $n\pi$. Therefore, the graph of the function $y = \sin x + x$ shows that $y \to x$ as the value of $\left| x \right|$increases.
The graph of the function is shown below:

Note:
The graph of the trigonometric function is obtained by finding the second derivative of the function. First, equate the first derivative of the function to obtain the value of x and then equate the second derivative of the function to zero to obtain the value of x. In such types of questions, students made mistakes to obtain the inflection points of the function which is further used to obtain the graph of the function.