Question

How do you graph $y=\sin x$ and $y=\cos x$ .

Answer 1

To draw the graph of $y=\sin x$ , we have to consider different values of x and find the corresponding values of y. We have consider $x=0,\pm \dfrac{\pi }{2},\pm \pi ,\pm \dfrac{3\pi }{2},\pm 2\pi$ and find the corresponding values of y. To draw the graph of $y=\cos x$ , we will do the similar procedure.

Complete step by step solution:
We have to graph $y=\sin x$ and $y=\cos x$ . Let us first consider $y=\sin x$ . We have to consider different values of x and find the corresponding values of y.
Let us consider $x=0$ . We have to substitute the value of x in $y=\sin x$ .
$\Rightarrow y=\sin 0=0$
Let us consider $x=\dfrac{\pi }{2}$ .
$\Rightarrow y=\sin \dfrac{\pi }{2}=1$
We have to consider $x=\pi$ .
$\Rightarrow y=\sin \pi =0$
Let us consider $x=\dfrac{3\pi }{2}$ .
$\Rightarrow y=\sin \dfrac{3\pi }{2}=-1$
We have to consider $x=2\pi$ .
$\Rightarrow y=\sin 2\pi =0$
Now, let us consider the negative values. So when $x=-\dfrac{\pi }{2}$
$\Rightarrow y=\sin \left( -\dfrac{\pi }{2} \right)$
We know that $\sin \left( -\theta \right)=-\sin \theta$ .
$\Rightarrow y=-\sin \left( \dfrac{\pi }{2} \right)=-1$
We have to consider $x=-\pi$ .
$\Rightarrow y=\sin \left( -\pi \right)=0$
Let us consider $x=-\dfrac{3\pi }{2}$ .
$\Rightarrow y=\sin \left( -\dfrac{3\pi }{2} \right)=-\sin \left( \dfrac{3\pi }{2} \right)=1$
We have to consider $x=-2\pi$ .
$\Rightarrow y=\sin \left( -2\pi \right)=0$
Let us tabulate these values.

x	$y=\sin x$
0	0
$\dfrac{\pi }{2}$	1
$\pi$	0
$\dfrac{3\pi }{2}$	-1
$2\pi$	0
$-\dfrac{\pi }{2}$	-1
$-\pi$	0
$-\dfrac{3\pi }{2}$	1
$-2\pi$	0

Now, let us plot the graph. Firstly, we have to plot the points in the graph. We have to convert $\pi$ into its numerical form, that is, 3.14 and plot the corresponding points. Then, we have to join the points as a curve. The graph of $y=\sin x$ is shown below.

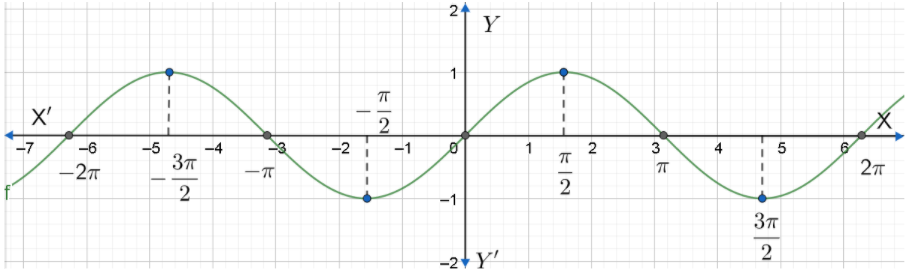
Now, let us consider $y=\cos x$ . Similar to the previous function, we will have to find the points to plot.
Let us consider $x=0$ . We have to substitute the value of x in $y=\cos x$ .
$\Rightarrow y=\cos 0=1$
Let us consider $x=\dfrac{\pi }{2}$ .
$\Rightarrow y=\cos \dfrac{\pi }{2}=0$
We have to consider $x=\pi$ .
$\Rightarrow y=\cos \pi =-1$
Let us consider $x=\dfrac{3\pi }{2}$ .
$\Rightarrow y=\cos \dfrac{3\pi }{2}=0$
We have to consider $x=2\pi$ .
$\Rightarrow y=\cos 2\pi =1$
Now, let us consider the negative values. So when $x=-\dfrac{\pi }{2}$
$\Rightarrow y=\cos \left( -\dfrac{\pi }{2} \right)$
We know that $\cos \left( -\theta \right)=\cos \theta$ .
$\Rightarrow y=\cos \left( \dfrac{\pi }{2} \right)=0$
We have to consider $x=-\pi$ .
$\Rightarrow y=\cos \left( -\pi \right)=\cos \pi =-1$
Let us consider $x=-\dfrac{3\pi }{2}$ .
$\Rightarrow y=\cos \left( -\dfrac{3\pi }{2} \right)=\cos \left( \dfrac{3\pi }{2} \right)=0$
We have to consider $x=-2\pi$ .
$\Rightarrow y=\cos \left( -2\pi \right)=\cos \left( 2\pi \right)=1$
Let us tabulate these values.

x	$y=\sin x$
0	-1
$\dfrac{\pi }{2}$	0
$\pi$	-1
$\dfrac{3\pi }{2}$	0
$2\pi$	1
$-\dfrac{\pi }{2}$	0
$-\pi$	-1
$-\dfrac{3\pi }{2}$	0
$-2\pi$	1

Now, let us plot the graph.

Note: We can also consider other angles also. Students have a chance of making mistakes by considering $\sin \left( -\theta \right)=\sin \theta$ and $\cos \left( -\theta \right)=-\cos \theta$ . We have considered the values of x to be $x=0,\pm \dfrac{\pi }{2},\pm \pi ,\pm \dfrac{3\pi }{2},\pm 2\pi$ as these values are easy to be plotted. We can find the domain and range of $y=\sin x$ and $y=\cos x$ . We know that the domain of a function is the complete set of possible values of the independent variable. Hence, the domain of sin x and cos x is $\left( -\infty ,\infty \right)$ . We know that range of a