Question

How do you graph $y=\sin \left( \theta \right)$ ?

Answer 1

From the given equation $y=\sin \left( \theta \right)$, try to find some values of ‘y’ corresponding to ‘$\theta$’. Put the values on a table. Using those values plot the graph and do the further analysis if necessary.

Complete step-by-step solution:
$y=\sin \left( \theta \right)$ is a trigonometric function.
For the graph of $y=\sin \left( \theta \right)$, we have to find some ‘y’ values for some corresponding ‘$\theta$’ values.
For some common values of ‘$\theta$’, ‘y’ can be calculated as follows
When $\theta =0$, $y=\sin 0=0$
When $\theta =\pm \dfrac{\pi }{2}$, $y=\sin \left( \pm \dfrac{\pi }{2} \right)=\pm 1$
When $\theta =\pm \pi$, $y=\sin \left( \pm \pi \right)=0$
When $\theta =\pm \dfrac{3\pi }{2}$, $y=\sin \left( \pm \dfrac{3\pi }{2} \right)=\pm 1$
When $\theta =\pm 2\pi$, $y=\sin \left( \pm 2\pi \right)=0$
And so on….
The above data can be collected in a table form as

$\theta$	0	$\pm \dfrac{\pi }{2}$	$\pm \pi$	$\pm \dfrac{3\pi }{2}$	$\pm 2\pi$
y	0	$\pm 1$	0	$\pm 1$	0

Using the above values of ‘y’ and ‘$\theta$’, the graph can be drawn as

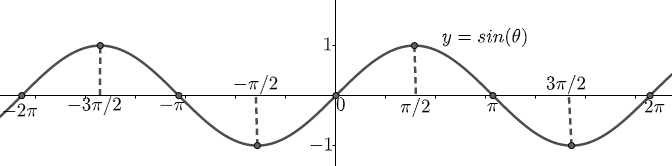
From the above graph, we can conclude that the graph crosses the ‘x’- axis at $\sin \left( \theta \right)=0$. So, the zeros of $y=\sin \left( \theta \right)$ are the multiples of ‘$\pi$’. $\sin \left( \theta \right)$ has the maximum value of 1 and the minimum value of $-1$ at the positive and negative odd multiplier of $\dfrac{\pi }{2}$ respectively.
This is the required solution.

Note: When the values of a function regularly repeat themselves, we say that the function is periodic. From the above graph we can notice that the values of $\sin \left( \theta \right)$ regularly repeat themselves in every $2\pi$ units. Therefore $\sin \left( \theta \right)$ is a periodic function with period ‘$2\pi$’. Since $\sin \left( -\theta \right)=-\sin \left( \theta \right)$, hence $y=\sin \left( \theta \right)$ is an odd function which is symmetrical with respect to the origin.