Question
Question: How do you graph \(y = \sin 2x + 1\) ?...
How do you graph y=sin2x+1 ?
Solution
The question is the form of y=asin(bx−c)+d. Here, we will find the amplitude, periods, phase shift, and vertical shift. The formula of amplitude is ∣a∣, the formula of the period is ∣b∣2π , the formula of phase shift is bc , and the formula of vertical shift is d. Find all the above values. Then take different values of x and find the values of y. After that, graph the trigonometric function using amplitude, period, phase shift, vertical shift, and the points.
Complete step by step answer:
In this question, the trigonometric function is given.
⇒y=sin2x+1
Compare the above equation with y=asin(bx−c)+d. And find all the values.
The value of ‘a’ is 1.
The value of ‘b’ is 2.
The value of ‘c’ is 0.
The value of ‘d’ is 1.
Now, let us find the value of amplitude.
As we already know, the value of the amplitude is ∣a∣.
Therefore,
⇒amplitude=∣a∣
Put the value of ‘a’ is 1.
⇒amplitude=∣1∣
⇒amplitude=1
Hence, the amplitude is 1.
Now, let us find the value of the period.
As we already know, the value of the period is∣b∣2π.
Therefore,
⇒period=∣b∣2π
Put the value of ‘b’ is 2.
⇒period=∣2∣2π
⇒period=22π
Cut the common factors from the numerator and the denominator.
⇒period=π
Hence, the period isπ.
Now, let us find the value of phase shift.
As we already know, the value of phase shift isbc.
Therefore,
⇒phase−shift=bc
Put the value of ‘b’ is 2, and the value of ‘c’ is 0.
⇒phase−shift=20
Therefore,
⇒phase−shift=0
Hence, the phase shift is 0.
Now, let us find the value of vertical shift.
As we already know, the value of vertical shift is d.
Therefore,
⇒vertical−shift=d
Put the value of ‘d’ is 1.
⇒vertical−shift=1
Hence, the vertical shift is 1.
Now, let us find the points.
For x=0
⇒y=sin2x+1
⇒y=sin2(0)+1
That is
⇒y=sin0+1
As we already know, sin0=0.
So,
⇒y=1
For x=4π
⇒y=sin2(4π)+1
That is
⇒y=sin(2π)+1
As we already know, sin2π=1.
So,
⇒y=2
For x=2π
⇒y=sin2(2π)+1
That is
⇒y=sinπ+1
As we already know, sinπ=0.
So,
⇒y=1
For x=43π
⇒y=sin2(43π)+1
That is
⇒y=sin23π+1
As we already know, sin23π=−1.
So,
⇒y=0
For x=π
⇒y=sin2(π)+1
That is
⇒y=sin2π+1
As we already know, sin2π=0.
So,
⇒y=1
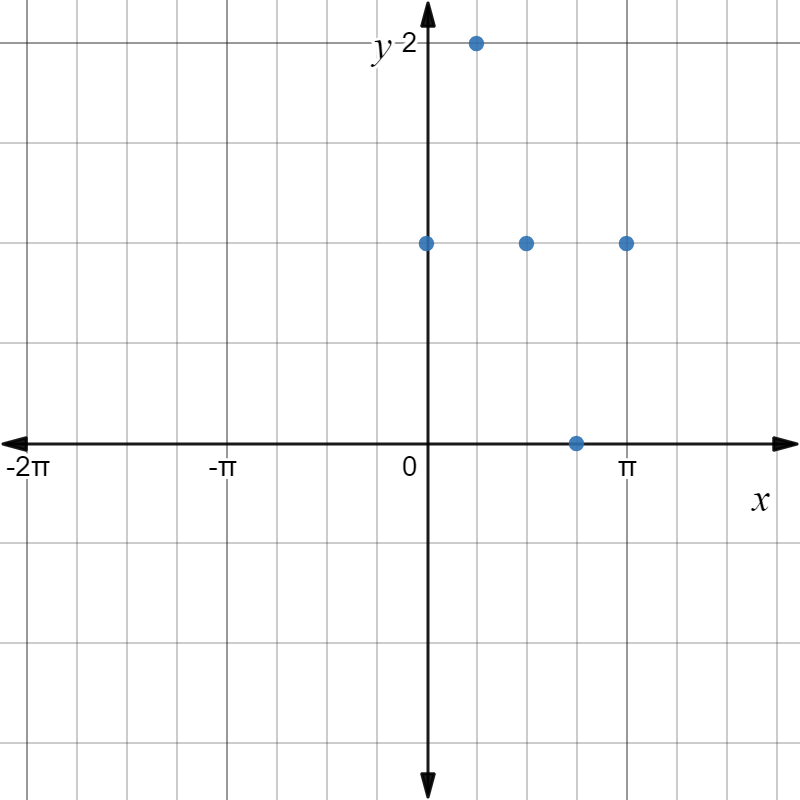
| X | 0 | 4π | 2π | 43π | π |
|---|---|---|---|---|---|
| y | 1 | 2 | 1 | 0 | 1 |
Note: We have to remember the trigonometry formula and trigonometry ratio values at the angle 0∘,30∘,45∘,60∘,90∘. And we have to remember the trigonometric function values in all quadrants.
In the first quadrant, sine and cosine functions are positive.
In the second quadrant, the sine function is positive and the cosine function is negative.
In the third quadrant, sine and cosine functions are negative.
In the fourth quadrant, the cosine function is positive and the sine function is negative.
