Question

How do you graph $y = \sin 2x$?

Answer 1

We need to graph the given function. We will use the domain and some values of $x$ lying between $- \pi$ and $\pi$ to find some values of $y$. Then, we will use the values of $y$ to find the coordinates of points lying on the required graph, and use the coordinates obtained to graph the function.

Complete step-by-step solution:
The domain of all sine functions is the set of all real numbers.
Thus, the domain of the function $y = \sin 2x$ is given by \left\\{ {x:x \in R} \right\\}. This means that the function $y = \sin 2x$ exists for all values of $x$, and is a continuous function.
Now, we will find some values of $y$ for some values of $x$ lying between $- \pi$ and $\pi$.
Substituting $x = - \pi$ in the function $y = \sin 2x$, we get
$\begin{array}{l}y = \sin \left( {2\left( { - \pi } \right)} \right)\\\ \Rightarrow y = \sin \left( { - 2\pi } \right)\end{array}$
The sine of an angle $- x$ can be written as $\sin \left( { - x} \right) = - \sin x$.
Simplifying the expression, we get
$\begin{array}{l} \Rightarrow y = - \sin \left( {2\pi } \right)\\\ \Rightarrow y = 0\end{array}$
Substituting $x = - \dfrac{{3\pi }}{4}$ in the function $y = \sin 2x$, we get
$\begin{array}{l} \Rightarrow y = \sin \left( {2\left( { - \dfrac{{3\pi }}{4}} \right)} \right)\\\ \Rightarrow y = \sin \left( { - \dfrac{{3\pi }}{2}} \right)\end{array}$
As sine function is an odd function, so we can writ above equation as
$\Rightarrow y = - \sin \left( {\dfrac{{3\pi }}{2}} \right)$
Substituting the value of the angle, we get
$\Rightarrow y = 1$
Substituting $x = - \dfrac{\pi }{2}$ in the function $y = \sin 2x$, we get
$\begin{array}{l} \Rightarrow y = \sin \left( {2\left( { - \dfrac{\pi }{2}} \right)} \right)\\\ \Rightarrow y = \sin \left( { - \pi } \right)\end{array}$
As sine function is an odd function, so we can writ above equation as
$\begin{array}{l} \Rightarrow y = - \sin \left( \pi \right)\\\ \Rightarrow y = 0\end{array}$
Substituting $x = - \dfrac{\pi }{4}$ in the function $y = \sin 2x$, we get
$\begin{array}{l} \Rightarrow y = \sin \left( {2\left( { - \dfrac{\pi }{4}} \right)} \right)\\\ \Rightarrow y = \sin \left( { - \dfrac{\pi }{2}} \right)\end{array}$
Substituting the value of the angle, we get
$\Rightarrow y = - 1$
Substituting $x = 0$ in the function $y = \sin 2x$, we get
$\begin{array}{l} \Rightarrow y = \sin \left( {2\left( 0 \right)} \right)\\\ \Rightarrow y = \sin \left( 0 \right)\end{array}$
Substituting the value of the angle, we get
$\Rightarrow y = 0$
Substituting $x = \dfrac{\pi }{4}$ in the function $y = \sin 2x$, we get
$\begin{array}{l} \Rightarrow y = \sin \left( {2\left( {\dfrac{\pi }{4}} \right)} \right)\\\ \Rightarrow y = \sin \left( {\dfrac{\pi }{2}} \right)\end{array}$
Substituting the value of the angle, we get
$\Rightarrow y = 1$
Substituting $x = \dfrac{\pi }{2}$ in the function $y = \sin 2x$, we get
$\begin{array}{l} \Rightarrow y = \sin \left( {2\left( {\dfrac{\pi }{2}} \right)} \right)\\\ \Rightarrow y = \sin \left( \pi \right)\end{array}$
Substituting the value of the angle, we get
$\Rightarrow y = 0$
Substituting $x = \dfrac{{3\pi }}{4}$ in the function $y = \sin 2x$, we get
$\begin{array}{l} \Rightarrow y = \sin \left( {2\left( {\dfrac{{3\pi }}{4}} \right)} \right)\\\ \Rightarrow y = \sin \left( {\dfrac{{3\pi }}{2}} \right)\end{array}$
Substituting the value of the angle, we get
$\Rightarrow y = - 1$
Substituting $x = \pi$ in the function $y = \sin 2x$, we get
$\begin{array}{l} \Rightarrow y = \sin \left( {2\left( \pi \right)} \right)\\\ \Rightarrow y = \sin \left( {2\pi } \right)\end{array}$
Substituting the value of the angle, we get
$\Rightarrow y = 0$
Arranging the values of $x$ and $y$ in a table and writing the coordinates, we get

$x$	$y$	$\left( {x,y} \right)$
$- \pi$	$0$	$\left( { - \pi ,0} \right)$
$- \dfrac{{3\pi }}{4}$	$1$	$\left( { - \dfrac{{3\pi }}{4},1} \right)$
$- \dfrac{\pi }{2}$	$0$	$\left( { - \dfrac{\pi }{2},0} \right)$
$- \dfrac{\pi }{4}$	$- 1$	$\left( { - \dfrac{\pi }{4}, - 1} \right)$
$0$	$0$	$\left( {0,0} \right)$
$\dfrac{\pi }{4}$	$1$	$\left( {\dfrac{\pi }{4},1} \right)$
$\dfrac{\pi }{2}$	$0$	$\left( {\dfrac{\pi }{2},0} \right)$
$\dfrac{{3\pi }}{4}$	$- 1$	$\left( {\dfrac{{3\pi }}{4}, - 1} \right)$
$\pi$	$0$	$\left( {\pi ,0} \right)$

Now, we will use the coordinates of the points to plot the required graph.
Plotting the graphs and joining the curve, we get

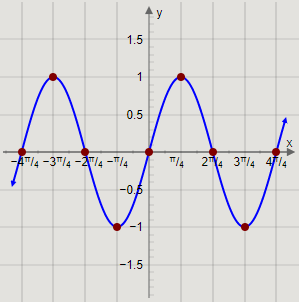
This is the required graph of the function $y = \sin 2x$.

Note:
The period of a function $y = \sin kx$ is given by $\dfrac{{2\pi }}{k}$. The period of the function $y = \sin 2x$ is $\dfrac{{2\pi }}{2} = \pi$. This means that the graph of $y = \sin 2x$ will repeat for every $\pi$ distance on the $x$-axis. It can be observed that the pattern and shape of the graph of $y = \sin 2x$ is the same from $- \pi$ to 0, and from 0 to $\pi$. The range of the sine function is from $- 1$ to 1.