Question

How do you graph $y=\sec \left( \dfrac{x}{2} \right)$?

Answer 1

We explain the main function of the given equation $y=\sec \left( \dfrac{x}{2} \right)$. We take the general equation and explain the amplitude, period. Then we equate the given function $y=\sec\left( \dfrac{x}{2} \right)$ with the general one and find the graph.

Complete step by step solution:
We need to find the amplitude, period for $y=\sec \left( \dfrac{x}{2} \right)$.
The main function of the given equation is $\sec x$. The period of $\cos x$ is $2\pi$.
We define the general formula to explain the amplitude, period for $\sec x$.
The $\sec x$ changes to $A\sec \left[ B\left( x+C \right) \right]+D$, the amplitude and the period becomes $\left| A \right|$ and $\dfrac{2\pi }{\left| B \right|}$.
Now we explain the things for the given $y=\sec \left( \dfrac{x}{2} \right)$.
$y=\sec \left( \dfrac{x}{2} \right)=1\times \sec \left[ \dfrac{1}{2}\times x \right]$. We equate with $A\sec \left[ B\left( x+C \right) \right]+D$.
The values will be $\left| A \right|=1;\left| B \right|=\dfrac{1}{2}$. The period is $\dfrac{2\pi}{\dfrac{1}{2}}=2\pi \times 2=4\pi$.
Therefore, the amplitude and period for $y=\sec \left( \dfrac{x}{2} \right)$ is $1,4\pi$ respectively.
The usual common graph which is easier to plot on the graph is $y=\sec x$.
The graph is an oscillating graph with boundary being $\left( -\infty ,-1 \right)$ and $\left( 1,\infty\right)$.
The domain for the graph $y=\sec x$ is $\mathbb{R}$.
The range for the graph $y=\sec x$ is $\mathbb{R}\backslash \left( -1,1 \right)$.

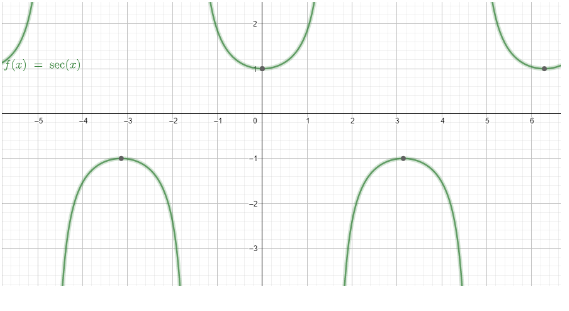
Now depending on the above-mentioned graph, we are going to first find the graph of
$y=\sec \left( \dfrac{x}{2} \right)$.
The change between $y=\sec x$ and $y=\sec \left( \dfrac{x}{2} \right)$ is that the graph is now stretched for twice its previous area.
The domain for the graph $y=\sec \left( \dfrac{x}{2} \right)$ is $\mathbb{R}$.
The range for the graph $y=\sec \left( \dfrac{x}{2} \right)$ is $\mathbb{R}\backslash \left( -1,1 \right)$.

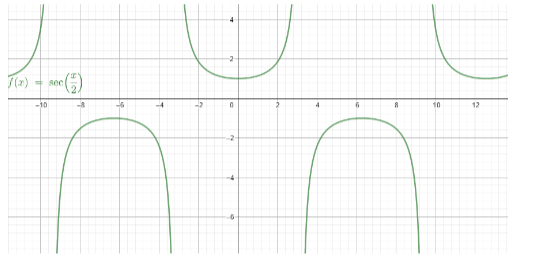
Note: Amplitude is the vertical distance from the X-axis to the highest (or lowest) point on a sin or cosine curve. Period of each generalized sine or cosine curve is the length of one complete cycle. The previous graphs were oscillating for an area of $\pi$ and now it’s for $2\pi$.