Question

How do you graph $y = {\log _5}\left( {2x + 2} \right) + 5$?

Answer 1

It is the graph of $y = {\log _5}x$ with a horizontal translation of 1 unit left, horizontal compression of $\dfrac{1}{2}$, and a vertical translation of 5 units up. To graph $y = {\log _5}x$, you can change it to an exponential equation, which would be ${5^y} = x$ and pick some values of $y$ to find $x$ values. This would give us the 'original' graph. $y = {\log _5}\left( {2x + 2} \right) + 5$ could be changed to $y = {\log _5}2\left( {x + 1} \right) + 5$.

Complete step-by-step solution:
It is the graph of $y = {\log _5}x$ with a horizontal translation of 1 unit left, horizontal compression of $\dfrac{1}{2}$, and a vertical translation of 5 units up!
To graph $y = {\log _5}x$, you can change it to an exponential equation, which would be ${5^y} = x$ and pick some values of $y$ to find $x$ values.
This would give us the 'original' graph.
$y = {\log _5}\left( {2x + 2} \right) + 5$ could be changed to $y = {\log _5}2\left( {x + 1} \right) + 5$
Select a few points to graph.
Find the point at $x = 0$.
Replace the variable $x$ with $0$ in the expression.
$f\left( 0 \right) = {\log _5}\left( {2\left( 0 \right) + 2} \right) + 5$
Simplify the result.
The exact value of ${\log _5}\left( 2 \right) = 0.43$.
$f\left( 0 \right) = 0.43 + 5$
$\Rightarrow f\left( 0 \right) = 5.43$
The final answer is $5.43$.
Find the point at $x = 1$.
Replace the variable $x$ with $1$ in the expression.
$f\left( 1 \right) = {\log _5}\left( {2\left( 1 \right) + 2} \right) + 5$
Simplify the result.
The exact value of ${\log _5}\left( 4 \right) = 0.86$.
$f\left( 1 \right) = 0.86 + 5$
$\Rightarrow f\left( 1 \right) = 5.86$
The final answer is $5.86$.
Find the point at $x = 2$.
Replace the variable $x$ with $2$ in the expression.
$f\left( 2 \right) = {\log _5}\left( {2\left( 2 \right) + 2} \right) + 5$
Simplify the result.
The exact value of ${\log _5}\left( 6 \right) = 1.11$.
$f\left( 2 \right) = 1.11 + 5$
$\Rightarrow f\left( 2 \right) = 6.11$
The final answer is $6.11$.
List the points in a table.

$x$	$y$
$0$	$5.43$
$1$	$5.86$
$2$	$6.11$

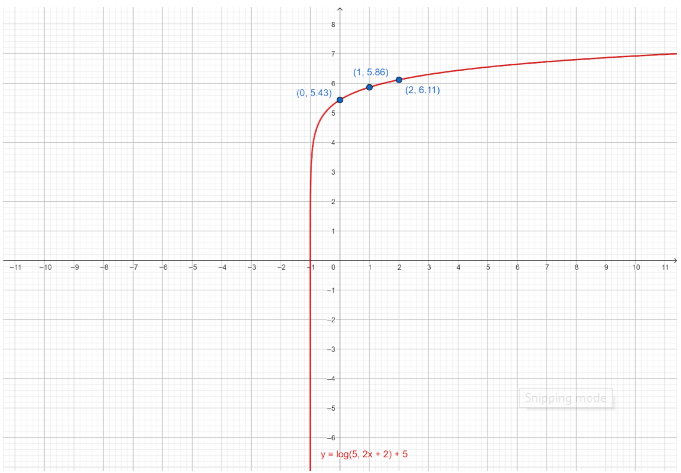
Note: From the graph, the transformed values are:
$K = - 1$, which means that the graph of $y = {\log _5}x$ is horizontally translated 1 unit left.
$D = 2$, which means that $y = {\log _5}x$ is horizontally compressed by a factor of $\dfrac{1}{2}$.
$H = 5$ which means that $y = {\log _5}x$ is vertically translated 5 units up.
Also note that due to these transformations, the vertical asymptote is translated 1 unit left, to $x = - 1$.