Question

How do you graph $y = \ln (x + 3)$ ?

Answer 1

To draw this graph $y = \ln (x + 3)$ at first, we have to know about the graph $y = \ln x$ . Then we have to see the point of intersection of $y = \ln x$ with $x$ -axis. Then we have to shift this point three times left of the $x$ axis and find out the point of intersection with the $y$ -axis, then our work will be easy.

Complete step-by-step solution:
First, we have to draw the graph $y = \ln x$ .
For that, we have to take some values of $x$ coordinate and find out the values of $y$ .
Let us take the values $0$ , $1$ , $e$ ( a specific number lies between $2$ and $3$ ; the value is approximate to $\;2.718$ ), $2$ and $5$ of $x$ .
Now we will find the values of $y$-axis for these values.
At $x = 0$ ;
From the equation $y = \ln x$ we will get;
$y = \ln 0$
$\Rightarrow y = \infty$
At $x = 1$ ;
From the equation $y = \ln x$ we will get;
$y = \ln 1$
$\Rightarrow y = 0$
At $x = e$ ;
From the equation $y = \ln x$ we will get;
$y = \ln e$
We know that $\ln e = 1$ .
$\Rightarrow y = 1$
At $x = 2$ ;
From the equation $y = \ln x$ we will get;
$y = \ln 2$
$\Rightarrow y = 0.693$
At $x = 5$ ;
From the equation $y = \ln x$ we will get;
$y = \ln 5$
$\Rightarrow y = 1.609$
Now we will plot these points $(0,\infty )$ , $(1,0)$ , $(e,1)$ , $(2,0.693)$ and $(5,1.609)$ in the two-dimensional coordinate system and we will get the graph of $y = \ln x$ .
To draw $y = \ln (x + 3)$ we just have to shift each point in the $x$ axis and then we can easily get the values of $y$ -axis. We will get the points $( - 3,\infty )$ , $( - 2,0)$ , $(e - 3,1)$ , $( - 1,0.693)$ and $(2,1.609)$ .
Now we will put these points and finally get;

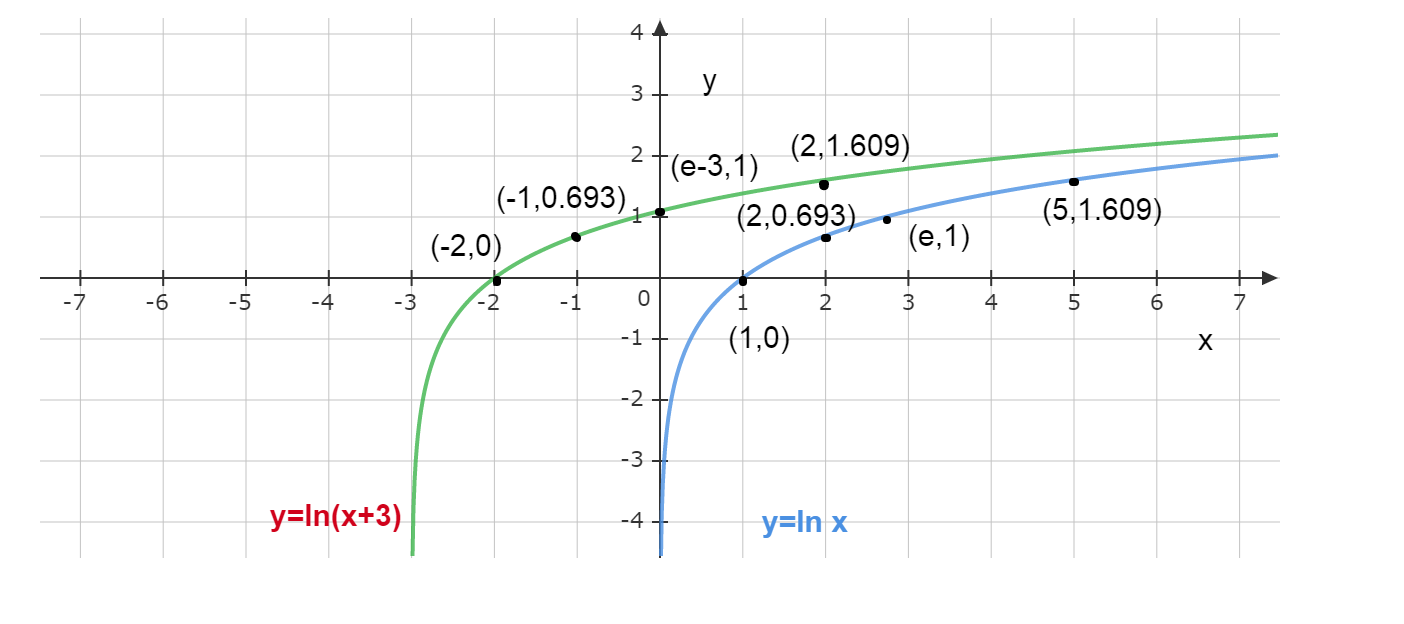
Here clearly $(0,\infty )$ and $( - 3,\infty )$ give the lower part of the graphs.

Note: Whenever we have this kind of plotting question at first we will try to find the nearest known function. Students should always be careful that $(0,\infty )$ and $( - 3,\infty )$ can’t be plotted. They only imply that the value of $x$ the graph will tend to infinity which means a never-ending end of the value of $y$ -axis.