Question

How do you graph $y = {\left( {\dfrac{1}{5}} \right)^x}$ ?

Answer 1

In this question, we are given an equation and we have to plot that equation on the graph. So, I suggest you find the intercepts first and plot those points on the graph. To find the intercepts, first, put $x = 0$, and then put $y = 0$. This will give you two points and then, you can plot them on the graph. After plotting the points, just connect the two points with a free hand and you will get the curve.

Complete step by step answer:
We are given an equation and we have to plot that equation on the graph. So, we will start by finding the points.
Point 1: We will put $x = 0$ and then we will find its $y$ coordinate.
$\Rightarrow y = {\left( {\dfrac{1}{5}} \right)^x}$
Putting$x = 0$, we will get –
$\Rightarrow y = {\left( {\dfrac{1}{5}} \right)^0} = 1$ (Any number raised to the power 0 is 1.)
Therefore, our point is $(0,1)$. Let us name this point as A.
Point 2: If we put $y = 0$, it won’t give us any point as our curve does not exist at $y = 0$.
So, what shall we do?
If we put $x = \infty$, what will we get?
$\Rightarrow y = {\left( {\dfrac{1}{5}} \right)^\infty }$
This value is undefined or we take it as $0$. This indicates that when $x$ is moving towards $\infty$, the value of y becomes very small (smaller than $1$ as y is equal to $1$ at $x = 0$). Thus, the graph will look like this –

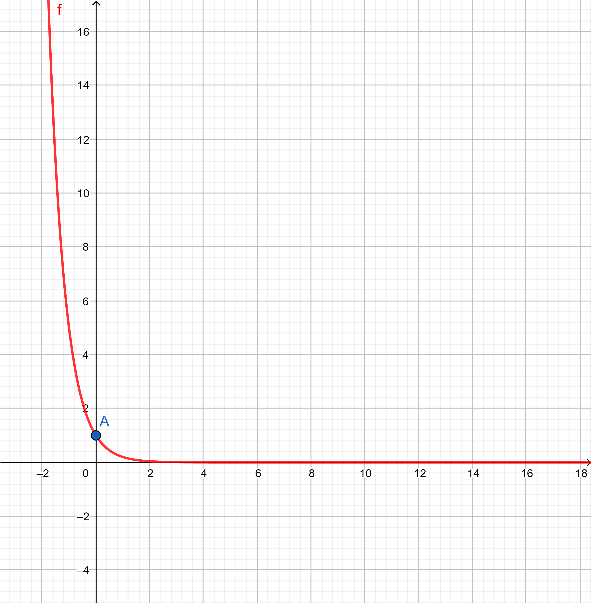
Note: Infinity is not a number, it’s a concept. When a number or a limit becomes so large that it is not possible to write it down or when it becomes undefined, we call it infinity
Same goes with the negative of infinity. When a number becomes too small to be defined, we call it negative infinity $\left( { - \infty } \right)$.