Question

How do you graph $y = {\left( {\dfrac{1}{3}} \right)^x} + 1?$

Answer 1

First, understand the given equation. Apply the $x$value in the given equation and find the corresponding $y$ value. We get a coordinate point$\left( {a,b} \right)$ on the given equation. Now plot the point in the graph and connect it. The equation to find the graph is a strictly decreasing and unbounded graph. The graph lies above the $x$ axis.

Complete answer:
Given equation is $y = {\left( {\dfrac{1}{3}} \right)^x} + 1$
This equation is exponential. In this equation to we draw a graph.
Assume that,
$x = - 3$apply the equation $y$
$y = {\left( {\dfrac{1}{3}} \right)^{ - 3}} + 1$
The first$\dfrac{1}{3}$ is a rational number. That number power value is a negative number generally ${\left( {\dfrac{1}{a}} \right)^{ - b}}$
So that we will give power separately numerator and denominator. It means

$$= {\left( {\dfrac{1}{3}} \right)^{ - 3}} + 1 \\\ = \dfrac{{{{\left( 1 \right)}^{ - 3}}}}{{{{\left( 3 \right)}^{ - 3}}}} + 1 \\\$$

In $1$ power any non-zero number the value is

$${\left( 1 \right)^a},\,a \ne 0 \\\ {\left( 1 \right)^a} = 1 \\\$$

So that ${\left( 1 \right)^{ - 1}} = 1$ and denominator ${\left( 3 \right)^{ - 3}},$
A non-zero number has a power value that is a negative number. We change to that nonzero in the denominator.
It means ${\left( a \right)^{ - b}}$ is a change to $\dfrac{1}{{{a^b}}}$
So that ${\left( 3 \right)^{ - 3}} = \dfrac{1}{{{3^3}}}$
Now the negative power value is converted to a positive power value. Now easily get the three power three is $27$
So that,

$$= \dfrac{1}{{{3^3}}} \\\ = \dfrac{1}{{27}} \\\$$

and $x = - 3$we get $y = 27 + 1$
because apply $1$ over $\dfrac{1}{{27}}$ is $27$

$$= 1 + 27 \\\ y = 28 \\\$$

So the point is $\left( { - 3,28} \right)$
$x = - 2$ apply the equation $y$

$$y = {\left( {\dfrac{1}{3}} \right)^{ - 2}} + 1 \\\ = {\left( {\dfrac{1}{3}} \right)^{ - 2}} + 1 \\\ = \dfrac{{{{\left( 1 \right)}^{ - 2}}}}{{{{\left( 3 \right)}^{ - 2}}}} + 1 \\\$$

So that ${\left( 3 \right)^{ - 2}} = \dfrac{1}{{{3^2}}}$
Now the negative power value is converted to a positive power value. Now easily get the three power two is $9$
So that,

$$= \dfrac{1}{{{3^2}}} \\\ = \dfrac{1}{9} \\\$$

and $x = - 2$apply to $y = 9 + 1$
$y = 10$
So the point is $\left( { - 2,10} \right)$
$x = - 1$ apply equation $y$

$$y = {\left( {\dfrac{1}{3}} \right)^{ - 1}} + 1 \\\ = {\left( {\dfrac{1}{3}} \right)^{ - 1}} + 1 \\\ = \dfrac{{{{\left( 1 \right)}^{ - 1}}}}{{{{\left( 3 \right)}^{ - 1}}}} + 1 \\\$$

So that ${\left( 3 \right)^{ - 1}} = \dfrac{1}{{{3^1}}}$
Now the negative power value is converted to a positive power value. Now easily get the three power one is $3$
So that,

$$= \dfrac{1}{{{3^1}}} \\\ = \dfrac{1}{3} \\\$$

and $x = - 1$we get $y = 3 + 1$
$y = 4$
So the point is $\left( { - 1,4} \right)$
$x = 0$ apply equation $y$

$$y = {\left( {\dfrac{1}{3}} \right)^0} + 1 \\\ = {\left( {\dfrac{1}{3}} \right)^0} + 1 \\\ = \dfrac{{{{\left( 1 \right)}^0}}}{{{{\left( 3 \right)}^0}}} + 1 \\\$$

So that ${\left( 3 \right)^0} = \dfrac{1}{{{3^0}}}$
Now easily get any constant number power zero is equal to one.
So that,

$$\dfrac{{{{\left( 1 \right)}^0}}}{{{{\left( 3 \right)}^0}}} = \dfrac{1}{1} \\\ = 1 \\\$$

and $x = 0$we get $y = 1 + 1$

$$= 1 + 1 \\\ y = 2 \\\$$

So the point is $\left( {0,2} \right)$
$x = 1$ apply equation $y$

$$y = {\left( {\dfrac{1}{3}} \right)^1} + 1 \\\ = {\left( {\dfrac{1}{3}} \right)^1} + 1 \\\ = \dfrac{{{{\left( 1 \right)}^1}}}{{{{\left( 3 \right)}^1}}} + 1 \\\$$ $$= \dfrac{{1 + 3}}{3} \\\ y = \dfrac{4}{3} \\\$$

So the point is $\left( {1,\dfrac{4}{3}} \right)$
$x = 2$ apply the equation $y$

$$y = {\left( {\dfrac{1}{3}} \right)^2} + 1 \\\ = \dfrac{{{{\left( 1 \right)}^2}}}{{{{\left( 3 \right)}^2}}} + 1 \\\$$ $$= \dfrac{{1 + 9}}{9} \\\ y = \dfrac{{10}}{9} \\\$$

So the point is $\left( {2,\dfrac{{10}}{9}} \right)$
$x = 3$ apply equation $y$

$$y = {\left( {\dfrac{1}{3}} \right)^3} + 1 \\\ = \dfrac{{{{\left( 1 \right)}^3}}}{{{{\left( 3 \right)}^3}}} + 1 \\\$$ $$= \dfrac{{1 + 27}}{{27}} \\\ y = \dfrac{{28}}{{27}} \\\$$

So the point is $\left( {3,\dfrac{{28}}{{27}}} \right)$
Now we mention the values in tabular format,

$x$	$- 3$	$- 2$	$- 1$	$0$	$1$	$2$	$3$
$y$	$28$	$10$	$4$	$2$	$\dfrac{4}{3}$	$\dfrac{{10}}{9}$	$\dfrac{{28}}{{27}}$

The Points are, $( - 3,28),( - 2,10),( - 1,4),(0,2),(1,\dfrac{4}{3}),(2,\dfrac{{10}}{9}),(3,\dfrac{{28}}{{27}})$
Then we get a graph of $y = {\left( {\dfrac{1}{3}} \right)^x} + 1$
The graph is given below

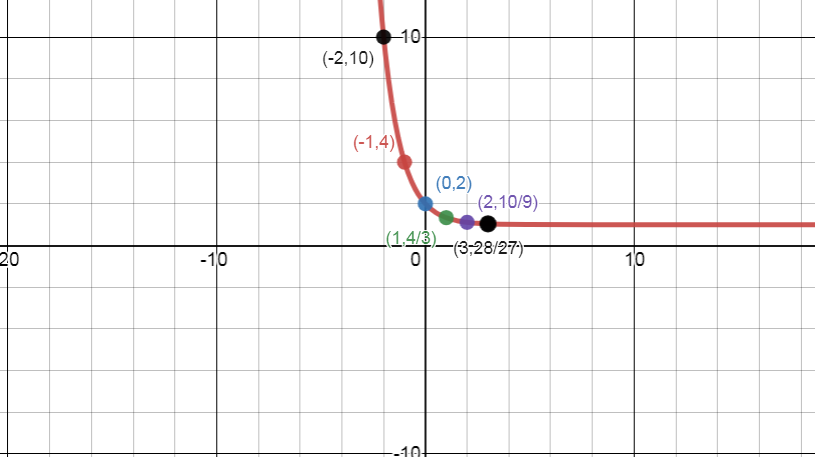
Note: Given problem is an exponential equation. The property of the exponential equation is unbounded. In ${a^x}$ and ${a^{ - x}}$ are the two forms of the exponent series. In ${a^x}$ and ${a^{ - x}}$ are strictly inequality forms. And that is strictly decreasing also. In the given equation the value $y$is always positive. Carefully labeled the point in the graph.