Question

How do you graph $y=\left| 2x+3 \right|$?

Answer 1

In this problem we need to draw the graph of the given equation $y=\left| 2x+3 \right|$. We can observe that the given equation is in modulus i.e., it will give only positive values of $y$ from the both the equations $y=2x+3$, $y=-2x-3$. So, we will draw the graphs of the both the lines $y=2x+3$, $y=-2x-3$ and we will consider only positive part of the both lines to show the graph of $y=\left| 2x+3 \right|$. To draw the graphs of the lines $y=2x+3$, $y=-2x-3$, we will first assume $y=0$ and calculates the value of $x$ and mark the points $\left( {{x}_{1}},0 \right)$, $\left( {{x}_{2}},0 \right)$ on the graph paper. Now we will assume $x=0$ and calculates the value of $y$ and mark the points $\left( 0,{{y}_{1}} \right)$, $\left( 0,{{y}_{2}} \right)$ on the graph paper. Now the line that joins the points $\left( {{x}_{1}},0 \right)$, $\left( 0,{{y}_{1}} \right)$ will represent the line $y=2x+3$ and the line that joins the points $\left( {{x}_{2}},0 \right)$, $\left( 0,{{y}_{2}} \right)$ will represent the line $y=-2x-3$. After plotting the graphs of the lines $y=2x+3$, $y=-2x-3$ we will eliminate the part of the graphs which is in negative of $y$ to show the graph of $y=\left| 2x+3 \right|$.

Complete step-by-step solution:
Given equation, $y=\left| 2x+3 \right|$.
We can write the equation $y=2x+3$, $y=-2x-3$ from the above given equation.
Substituting $y=0$ in the both equation and simplifying them, then we will get
$\begin{aligned} & 0=2x+3 \\\ & \Rightarrow -3=2x \\\ & \Rightarrow x=-1.5 \\\ \end{aligned}$ and $\begin{aligned} & 0=-2x-3 \\\ & \Rightarrow 2x=-3 \\\ & \Rightarrow x=-1.5 \\\ \end{aligned}$
Now the point $\left( -1.5,0 \right)$ lies on both the equations.
Substituting $x=0$ in the both equation and simplifying them, then we will get
$\begin{aligned} & y=2\left( 0 \right)+3 \\\ & \Rightarrow y=3 \\\ \end{aligned}$ and $\begin{aligned} & y=-2\left( 0 \right)-3 \\\ & \Rightarrow y=-3 \\\ \end{aligned}$
So, the point $\left( 0,3 \right)$ lies on $y=2x+3$, the point $\left( 0,-3 \right)$ lies on the line $y=-2x-3$.
Plotting the points on a graph paper and joining $\left( -1.5,0 \right)$, $\left( 0,3 \right)$ to get the line $y=2x+3$ as well as joining the points $\left( -1.5,0 \right)$, $\left( 0,-3 \right)$ to get the line $y=-2x-3$.

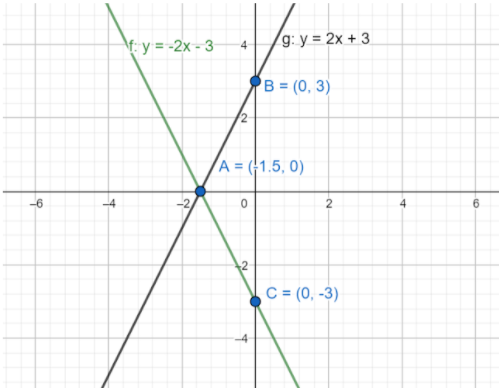
Now eliminating or neglecting the part of the graph which in negative $y$ to get the graph of $y=\left| 2x+3 \right|$.

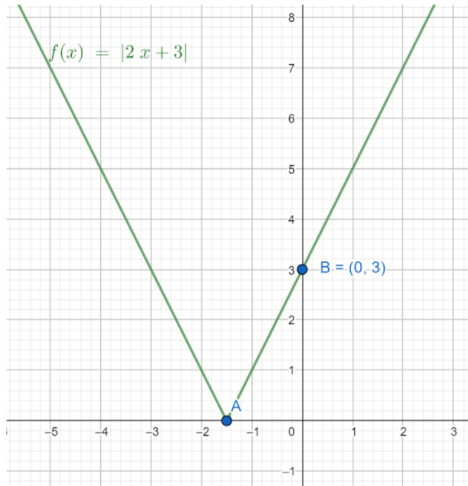
The above graph is our required graph.

Note: In the problem we have the equation like $y=\left| 2x+3 \right|$, so we have followed the above method. Instead of giving $y=\left| 2x+3 \right|$ if they have given $y=2x+3$ or $y=-2x-3$, then we will calculate the values of $x$ and $y$ when the other variables are zero and join those points to get the graph.