Question

How do you graph $y = {e^{\ln x}}$?

Answer 1

In the given question, we have been asked to graph the line $y = {e^{\ln x}}$. Now, this line is going to be a straight line. We have to first transform this equation into a simpler form. To do that, we are going to use the properties of a logarithm. Then we are going to solve this. To do that, we take a few points for solving the given expression. Then we plot those points on the graph. Then we just join the points and we get the answer.

Complete step by step answer:
The given equation is $y = {e^{\ln x}}$.
Taking $\ln$ on both sides,
$\ln y = \ln {e^{\ln x}}$
Now, we know that ${\log _b}{a^n} = n{\log _b}a$ and also, $\ln e = 1$
Thus, $\ln y = \ln x$
Hence, $y = x$.
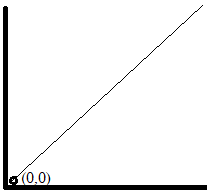
So, we have to graph the line of the equation$y = x$.
All the points on this graph are going to be of the form $\left( {h,h} \right)$.
But this graph can never go to $0$ or below (negative) because of the main equation $y = {e^{\ln x}}$, as,
${e^{{\rm{anything}}}} > 0$, hence, $y = {e^{something}} > 0$

Note:
So, for solving questions of such type, we first write what has been given to us. In this question, we only need to know one thing – how to get the points for the graph and then, how to plot the points on the graph. Then we just calculate the values from the equation, plot them on the graph, join the points on the graph and we get the line that marks the required equation. The logarithm function is a function that maps multiplication to addition. It is a point to note that ${e^x}$ and $\ln x$ never intersect.