Question

How do you graph $y = \dfrac{{\sin x}}{x}$?

Answer 1

The given trigonometric function is $y = \dfrac{{\sin x}}{x}$
We use the amplitude of oscillations in the given trigonometric function.
We put $x = 0$, and get the limit of the function at the origin.
After that we use the sampling function.
Finally we draw the graph.

Complete step-by-step solution:
The given trigonometric function is $y = \dfrac{{\sin x}}{x}$
The graph of $y = \dfrac{{\sin x}}{x}$ is one of decaying oscillations (oscillations of continuously decreasing amplitude).
The oscillations never stop, but go on decreasing in strength.
The amplitude of oscillations at any point $x$ is $\dfrac{1}{x}$.
The function $\dfrac{{\sin x}}{x}$ is not defined at $x = 0$.
Consequently, it makes sense to check the behavior of the function at the origin.
It turns out that the limit of the function at the origin exists.
$\Rightarrow \mathop {\lim }\limits_{x \to 0} \dfrac{{\sin x}}{x} = 1$
Hence, in the field of digital signal processing, you will come across something called the sampling function.
\Rightarrow Sa(x) = \left\\{ {\begin{array}{*{20}{c}} {\dfrac{{\sin x}}{x};x \ne 0} \\\ {\,1{\text{ }}\,\,\,;x = 0} \end{array}} \right.
So, called $\sin c$ function is different $\sin c(x) = Sa(\pi x)$
Therefore the point is that $\dfrac{{\sin x}}{x}$ is undefined at $x = 0$. So, its graph is as shown below. It is an even function.

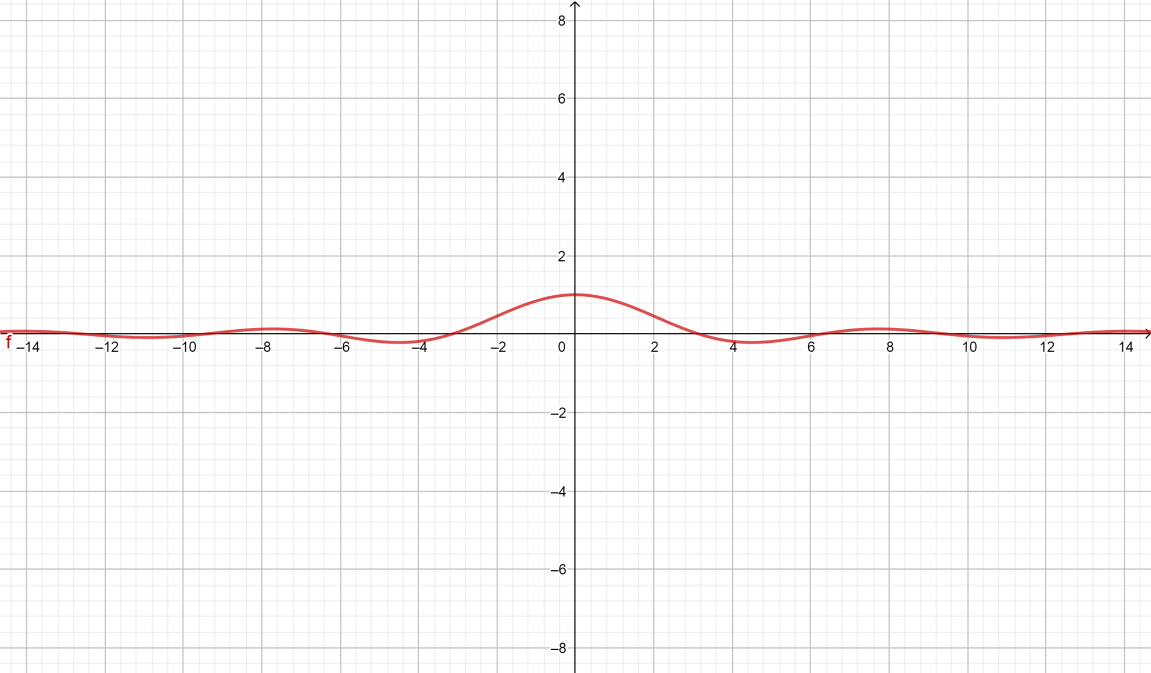
Note: The sine and cosine functions are useful for one very important reason, since they repeat in a regular pattern. There are vast arrays of things in and around us that repeat periodically. For example, the rising and setting of the sun, the motion of a spring up and down, the tides of the ocean and so on, are repeating at regular intervals of time. All periodic behavior can be studied through combinations of the sine and cosine functions.
Periodic functions are used throughout science to describe oscillations, waves and other phenomena that occur periodically.