Question

How do you graph $y=\dfrac{5}{4}x+5$ ?

Answer 1

The equation of $y=mx+c$ is the equation of a straight line so the graph of $y=mx+c$ is a straight line where m is the slope of line and c is the y intercept of line that means the straight line cuts the Y axis at (c,0)

Complete step by step answer:
The given equation in the question $y=\dfrac{5}{4}x+5$
We know that $y=mx+c$ is a straight line where the slope is m and $y=\dfrac{5}{4}x+5$ is in the same format as $y=mx+c$ so we can say $y=\dfrac{5}{4}x+5$ is a straight line so the graph of $y=\dfrac{5}{4}x+5$ will be a straight line
Here we can see $\dfrac{5}{4}$ is in the place of m so the value of slope is $\dfrac{5}{4}$ and the value of y intercept is 5 that means the straight line passes through (5,0)
We can draw the graph any straight line by using 2 point, 2 points is enough to draw the graph of straight line
First locate any 2 points on the Cartesian plane and join the 2 points to extend the line. That's it, the graph of straight is ready.
So let choose any 2 point we already know one point that is y intercept (5,0) let take another point $\left( 1,\dfrac{25}{4} \right)$
Let’s locate above those points in Cartesian plane and join them

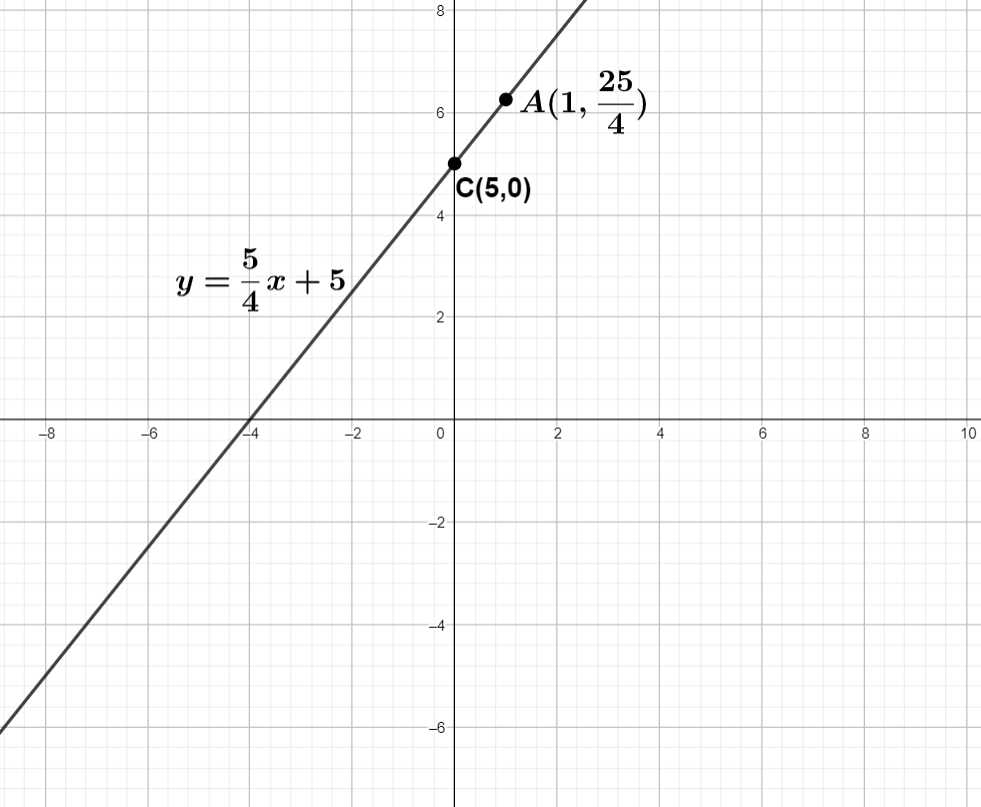
We can see C is the intercept and A is another point. We join the point and extend it . we got graph

Note:
The slope of the straight line $y=mx+c$ is m which is constant at all points. But if the equation of line is given in $ax+by+c=0$ where b is not equal to 0 then we can write it $y=-\dfrac{a}{b}x-\dfrac{c}{b}$ , now we can see the slope of the line is $-\dfrac{a}{b}$ and the y intercept is $-\dfrac{c}{b}$ where b is not equal to 0.