Question

How do you graph $y=\dfrac{3}{4}$ using intercepts?

Answer 1

To solve this problem, first if all we need to transform the given equation into its intercept form. After doing so, we compare it with the standard intercept form of a straight line. After comparing these two equations or forms, we can find out each intercept. Here, the y-intercept comes out to be $\dfrac{3}{4}$ and the x-intercept as infinite.

Complete step by step answer:
Every straight line equation can be expressed in the intercept form which is,
$\dfrac{x}{a}+\dfrac{y}{b}=1$ .... Equation 1
Where, $a$ is the x-intercept and $b$ is the y-intercept.
The equation of the straight line given in the question is,
$y=\dfrac{3}{4}$
Dividing both sides of the equation by $\dfrac{3}{4}$ we get,
$\dfrac{y}{\dfrac{3}{4}}=1$ .... Equation 2
In this equation 1, we find no term involving $x$. That means, the coefficient of the x-term is 0. In equation 1, the coefficient of the x-term is $\dfrac{1}{a}$ . Thus, comparing equation 2 with equation 1, we get
$\dfrac{1}{a}=0$
Taking reciprocal on both sides of the equation,
$a=\dfrac{1}{0}$
$a\to \infty$
This means that the x-intercept of this line is infinite, or it intersects the x-axis at infinity. In other words, this line is parallel to x-axis. Also, after comparing equation 1 and equation 2 , we see that $b=\dfrac{3}{4}$. This means that the y-intercept is $\dfrac{3}{4}$ .
Therefore, the line will be a line parallel to the x-axis with a y-intercept as $\dfrac{3}{4}$. The graph is shown below.

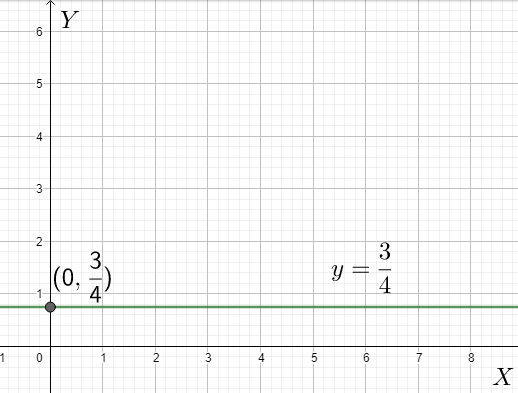
Note:
There is an alternate method to solve this problem. But, this requires us to have complete understanding of straight lines. The line given is
$y=\dfrac{3}{4}$
We can clearly see that this is a $y=c$ line, which means that whatever be the value of $x$, the corresponding value of $y$ remains the same. This indicates a line parallel to x-axis. The offset of this line from the x-axis is the constant value of the equation.