Question

How do you graph $y=\dfrac{2}{3}x-4$ ?

Answer 1

In the given question we were asked to solve $y=\dfrac{2}{3}x-4$ and find the x and y coordinate. So that we can plot the graph. We will use the formula of the slope-intercept form that is y = mx + b, to solve this problem. So let us see how we can solve this problem.

Step by step solution:
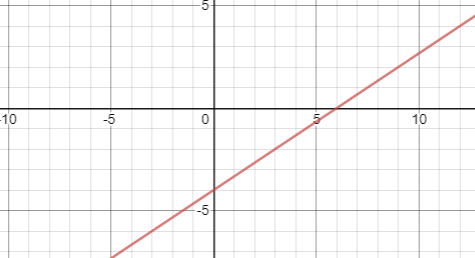
To solve the above equation, we will use the slope-intercept’s form formula that is y = mx + b, where m is the slope and b is the y-intercept. So as $y=\dfrac{2}{3}x-4$ this is a linear equation of the slope-intercept form, we get the slope as $\dfrac{2}{3}$ and the y-intercept as – 4.
The y-intercept is – 4, which means it is the value of y when x = 0. So we get the point (0, -4).
Also, we will get the x-intercept which is the value of x when y = 0.
Now, we will substitute 0 for y to find the value of x.
$\Rightarrow 0=\dfrac{2}{3}x-4$
After multiplying 3 on both sides
$\Rightarrow 3\times 0={3}\times \dfrac{2}{{{3}}}x-4\times 3$
After simplifying we get
$\Rightarrow 0=2x-12$
Adding 12 on both sides
$\Rightarrow 12=2x$
$\Rightarrow x=6$
Therefore, the x-intercept is (6, 0).

Note:
We have solved this question with slope-intercept form, but there are other forms of linear equations as well. Point-Slope form, Standard Form, and Intercept form. Also, note that in the above solution we considered the y-intercept as - 4 and did not neglect the minus sign. So we need to take care that we do not miss any sign.