Question

How do you graph $y=-\dfrac{2}{3}x+1$ ?

Answer 1

Here we need to find the graph for the given equation and we know that this is an equation of a straight line and the given equation is written in the slope-intercept form. So from there, we will get the value of the slope of the line and then the $y$ intercept. Then we will find the value of the $x$ intercepts by putting the value of $y$ as zero. Then using the slope and the intercepts, we will draw the graph accordingly.

Complete step by step solution:
Here we need to find the graph for the given equation and the given equation is $y=-\dfrac{2}{3}x+1$.
We know that this is an equation of a straight line and the given equation is written in the slope-intercept form.
We know that the slope-intercept form of an equation is given by $y=mx+b$
Here, $m$ is the slope of the line and $b$ is the $y$ intercept.
Now, we will compare this equation with the given equation.
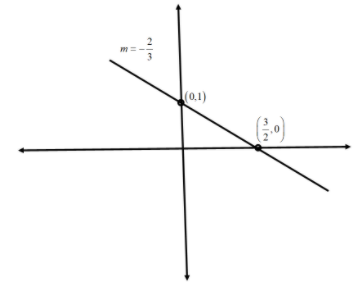
Slope in this case is $\dfrac{{ - 2}}{3}$ and $y$ intercept is equal to 1.
Now, we will find the $x$ intercepts by putting the value of $y$ as zero.
$0=-\dfrac{2}{3}x+1$
Now, we will subtract 1 from both sides.
$\Rightarrow 0-1=-\dfrac{2}{3}x+1-1$
On further simplification, we get
$\Rightarrow - 1 = - \dfrac{2}{3}x$
Now, we will divide both sides by $\dfrac{{ - 2}}{3}$
$\Rightarrow \dfrac{{ - 1}}{{ - \dfrac{2}{3}}} = \dfrac{{ - \dfrac{2}{3}x}}{{ - \dfrac{2}{3}}}$
On further simplification, we get
$\Rightarrow \dfrac{3}{2} = x \\\ \Rightarrow x = \dfrac{3}{2} \\\$
Therefore, the $x$ intercept is equal to $\dfrac{3}{2}$.
Now, we will draw the graph using the slope and the intercepts.

Note:
Here we have obtained the value of the slope of the line using the slope-intercept form of the equation. The slope of a line is defined as the value which measures the steepness of the line or the inclination of the line with the $x$ axis. We know that the graph of a linear equation is always a straight line whereas the graph of a quadratic equation is always a curve. We can draw the graph of an equation by using the different points which are obtained by substituting different values of $x$ and $y$ in the equation.